1. NumPy

Contents

1. NumPy#

1. Introduction#

Numpy stands for Numerical python and it is typically imported as np

import numpy as np

The major data structure numpy provides is the array, or more accurately ndarray, and arrays can represent data in multiple Dimensions. Section 9 of this tutorial goes over several other types of data structures but we will focus on the array.

1.1: Features of an Array#

  • Homgeonous Data Type (Structured Arrays can have multiple data types but store data differently)

  • Once created size can not be changed

  • Must be rectangular

1.2: Array Dimensionality#

Dimension (Rank)

Common Name

Description

Example Shape (.shape)

0D

Scalar

A single numerical value, not an array but an atomic element.

() (empty tuple)

1D

Vector

A one-dimensional array (list-like but with array properties).

(n,) (e.g., (5,))

2D

Matrix

A rectangular grid of numbers with rows and columns.

(m, n) (e.g., (3, 4))

3D

Tensor

A stack of matrices, used in physics and deep learning.

(d, m, n) (e.g., (2, 3, 4))

4D

HyperTensor

Higher-order tensor, used in advanced machine learning.

(t, d, m, n) (e.g., (5, 2, 3, 4))

nD

nD Array (General)

An array with any number of dimensions (n ≥ 0).

(dim_1, dim_2, ..., dim_n)


Array Axes#

An axes is a dimension along which data is arranged in a NumPy array and you can think of it as an indexing direction that allows you to navigate and manipulate data. Note, axis 0 is the highest ranked axes.

Dimension (Rank)

Axes

Description

1D Array

1 axis (axis 0)

Like a Python list: a single sequence of elements.

2D Array

2 axes (axis 0: rows, axis 1: columns)

Like a table (rows and columns).

3D Array

3 axes (axis 0: depth, axis 1: rows, axis 2: columns)

Like multiple stacked tables.

4D array Example#

Multiple experiments of the spectra of a reaction mixture where reactants concentrations are varied.

Axis

Description

Role in Experiment

Axis 0

Experiment Number

Separate runs where reactant concentrations vary

Axis 1

Temporal Data Cube

Absorbance values at different times

Axis 2

Wavelength

Spectral dimension (e.g., 400-700 nm)

Axis 3

Absorbance at Wavelength

Intensity values at each wavelength


Since NumPy indexing follows axes, so you can retrieve meaningful slices from your data.


1.3 Array Properties#

Arrays use brackets like lists and in fact a 1D array looks like a list, but the array holds one block of memory while the list has pointers to multiple memory blocks.

  1. Fixed Data Type (All elements of same data type)

  2. Arrays are Mutable (You can change values within an array)

  3. Fixed Size (Fixed upon creation)

  4. Efficient Memory Usage (stores data in contiguous memory)

  5. Vectorized Operations (supports element-wise operations that a list would require loops for)

  6. Multi-Dimensional Support (Does not need nested structures like a list would)

2. Arrays as a Python Objects#

Table of NumPy Array Attributes#

Attribute

Description

shape

Tuple of array dimensions

ndim

Number of array dimensions

size

Total number of elements in the array

dtype

Data type of the array elements

itemsize

Size in bytes of each array element

data

Python buffer object pointing to the array’s data

strides

Tuple of bytes to step in each dimension when traversing the array

flags

Information about the memory layout of the array

real

Real part of the array (for complex number arrays)

imag

Imaginary part of the array (for complex number arrays)

Table of NumPy Array Methods#

Method

Description

reshape()

Returns a new array with a changed shape

transpose()

Returns a new array with axes transposed

flatten()

Returns a copy of the array collapsed into one dimension

astype()

Cast the array to a specified data type

copy()

Return a copy of the array

fill()

Fill the array with a scalar value

sort()

Sort an array in-place

max()

Return the maximum value along a given axis

min()

Return the minimum value along a given axis

mean()

Compute the arithmetic mean along the specified axis

Table of NumPy Functions for Arrays#

Function

Description

np.array()

Create an array

np.zeros()

Create an array filled with zeros

np.ones()

Create an array filled with ones

np.arange()

Create an array with evenly spaced values within a given interval

np.linspace()

Create an array with evenly spaced numbers over a specified interval

np.concatenate()

Join arrays along an existing axis

np.vstack()

Stack arrays vertically (row-wise)

np.hstack()

Stack arrays horizontally (column-wise)

np.split()

Split an array into multiple sub-arrays

np.where()

Return elements chosen from two arrays depending on condition

3. Array Data Types#

dtype()#

In python everything has a type, which you can find with the type() function. In Numpy data also has a type function called dtype(), which like the type(), defines how much memory the object uses. The following table covers the common data types stored in a Numpy Array and it is often important to define these when creating an array.

Code

Data Type

Example Equivalent

'b'

Boolean

bool

'i'

Integer (default)

int32, int64 (depends on system)

'L'

Long Integer

int64 (platform-dependent)

'u'

Unsigned Integer

uint32, uint64

'f'

Floating Point

float32, float64

'c'

Complex Float

complex64, complex128

'm'

Timedelta

N/A

'M'

Datetime

N/A

'O'

Object (Python objects)

N/A

'S' or 'a'

String (bytes)

Fixed-length strings

'U'

Unicode String

Fixed-length Unicode

.astype() -changing dtypes#

import numpy as np

# Example array of long integers
arr = np.array([1733976600, 1733798400], dtype='l')

# Convert to float
arr_float = arr.astype('f8')  # Convert to float64

import numpy as np

# Example array
arr = np.array([1733976600, 1733798400], dtype='l')

# Check dtype
print(arr)
print(arr.dtype)  
print(f'memory location = {id(arr)}\n')
# Convert to float
arr_float = arr.astype('f8')  # Convert to float64
print(arr_float)
print(arr_float.dtype)
print(f'memory location = {id(arr_float)}')

[1733976600 1733798400]
int64
memory location = 130959724447856

[1.7339766e+09 1.7337984e+09]
float64
memory location = 130958383798800

4. Basic Array Tasks#

4.1: Creating Arrays#

Array syntax looks like a Python list for a 1D Array in that the elements are in square brackets and separated by commas.

Array constructor (np.array())#

Creating Arrays from other python objects. In this exercise we are going to use nested python lists to create an array with the array constructor np.array().

note, an ndarray is of a single type of data, but you can use the np.array() constructor to make a structured array, which is an array with more than one data type (see section 9 below).

1D array#

import numpy as np
my_list = [1,2,3,4,5,6,7,8]
print(f"{my_list} is {type(my_list)}.")
my_1Darray=np.array(my_list)
print(f"{my_1Darray} is {type(my_1Darray)}.")

[1, 2, 3, 4, 5, 6, 7, 8] is <class 'list'>.
[1 2 3 4 5 6 7 8] is <class 'numpy.ndarray'>.

Just as a loop an be nested inside of another loop, a list can be nested inside of another list

2D array#

my_2nested_list = [[1,2],[3,4],[5,6],[7,8]]
print(f"{my_2nested_list} is {type(my_2nested_list)}.")
my_2Darray=np.array(my_2nested_list)
print(f"{my_2Darray} is {type(my_2Darray)}.")

[[1, 2], [3, 4], [5, 6], [7, 8]] is <class 'list'>.
[[1 2]
 [3 4]
 [5 6]
 [7 8]] is <class 'numpy.ndarray'>.

3D array#

my_3nested_list = [[[1,2],[3,4]],[[5,6],[7,8]]]
print(f"{my_3nested_list} is {type(my_3nested_list)}.")
my_3Darray=np.array(my_3nested_list)
print(f"{my_3Darray} is {type(my_3Darray)}.")

[[[1, 2], [3, 4]], [[5, 6], [7, 8]]] is <class 'list'>.
[[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]] is <class 'numpy.ndarray'>.

np.linespace()#

  • generates evenly spaced numbers over a specified range.

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

Parameter

Description

start

The starting value of the sequence (inclusive).

stop

The ending value of the sequence. By default, it is inclusive, but you can exclude it using endpoint=False.

num

The number of points to generate (default = 50).

endpoint

If True (default), the stop value is included in the sequence. If False, the stop value is excluded.

retstep

If True, returns the spacing (step size) between values in addition to the array.

dtype

The desired NumPy data type for the output array.

 
# np.linspace(): 5 evenly spaced numbers
print("linspace:", np.linspace(1, 10, num=5))
# Output: [ 1.  3.25  5.5  7.75 10. ]

linspace: [ 1.    3.25  5.5   7.75 10.  ]

np.arange()#

  • gives evenly spaced value over a range with control of step size and data value.

np.arange(start, stop, step=1, dtype=None)

Parameter

Description

start

The starting value (inclusive). Defaults to 0 if not provided.

stop

The ending value (exclusive by default).

step

The increment (default = 1). Controls how the sequence progresses.

dtype

The data type of the output array. If not specified, NumPy infers it automatically.

 
import numpy as np

# np.arange(): Step size of 2
print("arange:", np.arange(1, 10, 2))  
# Output: [1 3 5 7 9]

arange: [1 3 5 7 9]

Comparison: np.arange() vs. np.linspace()#

Feature

np.arange()

np.linspace()

Step Control

Uses a fixed step between values.

Uses a fixed number of points between start and stop.

Stop Inclusion

Exclusive (default behavior).

Inclusive (by default), unless endpoint=False.

Flexibility

Good for integer-based sequences with regular spacing.

Better for floating-point sequences with exact spacing.

Use Case

When you know the step size and want values to progress by that amount.

When you know the number of points and want them distributed evenly.

Example

np.arange(1, 10, 2) → [1, 3, 5, 7, 9]

np.linspace(1, 10, num=5) → [ 1.  3.25  5.5  7.75 10. ]

 
import numpy as np

# np.arange(): Step size of 2
print("arange:", np.arange(1, 10, 2))  
# Output: [1 3 5 7 9]

# np.linspace(): 5 evenly spaced numbers
print("linspace:", np.linspace(1, 10, num=5))
# Output: [ 1.  3.25  5.5  7.75 10. ]

arange: [1 3 5 7 9]
linspace: [ 1.    3.25  5.5   7.75 10.  ]

np.zeros()#

This function allows you to quickly create an array filled with zeros,

np.zeros((2))

array([0., 0.])

np.zeros((3,2))

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

np.zeros((4,3,2))

array([[[0., 0.],
        [0., 0.],
        [0., 0.]],

       [[0., 0.],
        [0., 0.],
        [0., 0.]],

       [[0., 0.],
        [0., 0.],
        [0., 0.]],

       [[0., 0.],
        [0., 0.],
        [0., 0.]]])

np.ones()#

np.ones((2,3,4))

array([[[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]],

       [[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]]])

4.2: Array Indexing (Introduction)#

Indexing goes along the axes from zero to “n” for an “n” dimensional array. So a 3D array would be sheet, column, row. Let’s create a 3D NumPy array representing absorbance values at different wavelengths over time for multiple experiments.

  • Axis 0 → Experiment number

  • Axis 1 → Sample Times

  • Axis 2 → Wavelengths

import numpy as np

# Create a 3D array: 2 experiments, 4 sample times, 3 wavelengths
data = np.array([
    [[0.12, 0.15, 0.18], [0.14, 0.17, 0.20], [0.16, 0.19, 0.22], [0.18, 0.21, 0.24]],  # Experiment 1
    [[0.22, 0.25, 0.28], [0.24, 0.27, 0.30], [0.26, 0.29, 0.32], [0.28, 0.31, 0.34]]   # Experiment 2
])

print("Shape of the array:", data.shape)  # (2, 4, 3)
print(data)

Shape of the array: (2, 4, 3)
[[[0.12 0.15 0.18]
  [0.14 0.17 0.2 ]
  [0.16 0.19 0.22]
  [0.18 0.21 0.24]]

 [[0.22 0.25 0.28]
  [0.24 0.27 0.3 ]
  [0.26 0.29 0.32]
  [0.28 0.31 0.34]]]

This array has:

  • 2 experiments (Axis 0)

  • 4 time steps (Axis 1)

  • 3 wavelengths (Axis 2)

Extracting a Single Value#

To get a single absorbance value for Experiment 2, sample time 3, Wavelength 2:

value = data[1, 2, 1]  # Experiment 2 (index 1), Time step 3 (index 2), Wavelength 2 (index 1)
print("Absorbance value:", value)

Absorbance value: 0.29

Extract a 1D array#

Obtain all absorbances for the first experiment at the second time step

time_2_exp_1 = data[0, 1, :]
print(time_2_exp_1)

[0.14 0.17 0.2 ]

Extract a 2D array#

Obtain absorbance values at third wavelength for all experiments and all sample times

wavelength_3 = data[:, :, 2]
print(wavelength_3)

[[0.18 0.2  0.22 0.24]
 [0.28 0.3  0.32 0.34]]

Slice out the first experiment#

subset = data[0:1, :, :]
print(subset.shape)  
print(subset)

(1, 4, 3)
[[[0.12 0.15 0.18]
  [0.14 0.17 0.2 ]
  [0.16 0.19 0.22]
  [0.18 0.21 0.24]]]

Slice out all data for second and third sample times#

subset_time = data[:, 1:3, :]
print(subset_time.shape)
print(subset_time)

(2, 2, 3)
[[[0.14 0.17 0.2 ]
  [0.16 0.19 0.22]]

 [[0.24 0.27 0.3 ]
  [0.26 0.29 0.32]]]

Summary Table#

Operation

Code

Output Shape

Single Value

data[1, 2, 1]

() (Scalar)

1D Time Slice

data[0, 1, :]

(3,)

Wavelength 3 Absorbance

data[:, :, 2]

(2, 4)

First Experiment

data[0:1, :, :]

(1, 4, 3)

Time Steps 2-3

data[:, 1:3, :]

(2, 2, 3)

Every Other Wavelength

data[:, :, ::2]

(2, 4, 2)

4.3: Array Attributes#

.shape#

Gives the shape of the array

my_array=np.ones((4,3,2))
my_array.shape

(4, 3, 2)

.ndim#

Gives the number of dimensions

my_array.ndim

3

.size#

Gives total number of elements in an array

my_array.size

24

4.4: Arrays from Functions (np.fromfunction())#

You can make an array from a function, let’s create an array for the molar mass of 1-10 elements of carbon, oxygen and hydrogen.

import numpy as np
def molar_mass_grid(element_idx, atom_count):
    # Atomic masses: C=12.01, H=1.008, O=16.00
    atomic_masses = np.array([12.01, 1.008, 16.00])  
    return atomic_masses[element_idx.astype(int)] * (atom_count + 1)

mass_grid = np.fromfunction(molar_mass_grid, (3,10), dtype=float)
print(mass_grid)

[[ 12.01   24.02   36.03   48.04   60.05   72.06   84.07   96.08  108.09
  120.1  ]
 [  1.008   2.016   3.024   4.032   5.04    6.048   7.056   8.064   9.072
   10.08 ]
 [ 16.     32.     48.     64.     80.     96.    112.    128.    144.
  160.   ]]

import numpy as np

# Step 1: Define the mass grid using np.fromfunction()
def molecular_mass_grid(element_idx, atom_count):
    atomic_masses = np.array([12.01, 1.008, 16.00])  # C, H, O
    return atomic_masses[element_idx.astype(int)] * (atom_count + 1)

mass_grid = np.fromfunction(molecular_mass_grid, (3, 10), dtype=float)

# Step 2: Define a function to compute molar mass
def compute_molar_mass(formula):
    # Define mapping for element index lookup
    element_indices = {'C': 0, 'H': 1, 'O': 2}
    
    # Parse formula into element counts
    parsed_formula = [('C', 3), ('H', 8), ('O', 1)]  # Example: C3H8O

    # Step 3: Compute molar mass
    #molar_mass = sum(mass_grid[element_indices[element], atoms - 1] for element, atoms in parsed_formula)
    molar_mass = 0  # Initialize molar mass
    for element, atoms in parsed_formula:
        element_idx = element_indices[element]  # Get index for the element
        molar_mass += mass_grid[element_idx, atoms - 1]  # Accumulate mass using array indexing
        
    return molar_mass

# Step 4: Compute molar mass of C3H8O (Propanol)
molar_mass_C3H8O = compute_molar_mass("C3H8O")
print(f"Molar Mass of C3H8O: {molar_mass_C3H8O:.2f} g/mol")

Molar Mass of C3H8O: 60.09 g/mol

4.5: Sorting Arrays#

  • axis=0: Sort along columns (vertically)

  • axis=1: Sort along rows (horizontally)

  • axis=-1: Sort along the last axis (default)

import numpy as np

arr = np.array([[3, 1, 4], [1, 5, 9], [2, 6, 5]])
print(f'original array: \n{arr}\n')
# Sort each column

print(f'sort axis 0 \n{np.sort(arr, axis=0)}\n')

# Sort each row
print(f'sort axis 1 \n {np.sort(arr, axis=1)}')

original array: 
[[3 1 4]
 [1 5 9]
 [2 6 5]]

sort axis 0 
[[1 1 4]
 [2 5 5]
 [3 6 9]]

sort axis 1 
 [[1 3 4]
 [1 5 9]
 [2 5 6]]

4.6 Reshaping Arrays#

.reshape()#

  • The number of elements of the original and reshaped arrays must be the same

  • (3,2,4) array must be a multiple of the product of the indices

  • In the following we have measurements at 5 wavelengths taken 3 different times

# Simulated absorbance data (1D)
absorbance_data = np.arange(15)  # Example: 15 absorbance values
print(absorbance_data)
# Reshape into 3 time points × 5 wavelengths
absorbance_matrix = absorbance_data.reshape(3, 5)

print(absorbance_matrix)

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]
[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]

.flatten()#

-convert multi-dimensional array to a 1D array

print(absorbance_matrix)
flat_matrix=absorbance_matrix.flatten()
print(flat_matrix)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]

Transpose Arrays#

Transposing a matrix swaps columns and rows. For dimensions higher than 2 you have two choices, .T and .transpose(). The former does a full transpose and completely rearranges the order, while the latter allows you to specify axes transposed .T vs. .transpose(): Key Differences

Feature

.T (Shortcut)

.transpose() (Flexible)

Works on 2D?

Yes (swaps rows & columns)

Yes (same as .T for 2D)

Works on 3D+?

Yes (reverses all axes)

Yes (custom axis order)

Custom Axis Order?

No

Yes (.transpose(axes))

Effect on (2,3,4) Shape?

➝ (4,3,2) (full reverse)

➝ Custom order (e.g., (3,4,2))

.T (Full Transpose)#

Full transpose

my_array=np.arange(1,25).reshape(6,4)
print(my_array)
print(f'\ntransposed array \n{my_array.T}')

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]
 [21 22 23 24]]

transposed array 
[[ 1  5  9 13 17 21]
 [ 2  6 10 14 18 22]
 [ 3  7 11 15 19 23]
 [ 4  8 12 16 20 24]]

.transpose()#

my_array=np.arange(1,25).reshape(2,3,4)
print(my_array)
print(f'transposing rows (3) and columns(1) of 3D array \n{my_array.transpose(0,2,1)}')

[[[ 1  2  3  4]
  [ 5  6  7  8]
  [ 9 10 11 12]]

 [[13 14 15 16]
  [17 18 19 20]
  [21 22 23 24]]]
transposing rows (3) and columns(1) of 3D array 
[[[ 1  5  9]
  [ 2  6 10]
  [ 3  7 11]
  [ 4  8 12]]

 [[13 17 21]
  [14 18 22]
  [15 19 23]
  [16 20 24]]]

Scenario: Kinetic Absorbance Data for a Chemical Reaction#

A spectrometer records absorbance at multiple wavelengths over several time points across different experiments (e.g., varying reagent concentrations).
This dataset is stored in a 3D NumPy array where:

  • Axis 0 → 3 different experiments (e.g., different NaOH concentrations).

  • Axis 1 → 4 different time points (e.g., 0s, 10s, 20s…).

  • Axis 2 → 5 different wavelengths (e.g., 400 nm, 450 nm, 500 nm…).

Goal: The chemist needs to rearrange the dataset to focus on a wavelength-first structure, where:

  • Axis 0 → Wavelengths

  • Axis 1 → Experiments

  • Axis 2 → Time points

This makes it easier to extract and compare spectral changes at specific wavelengths.

import numpy as np

np.random.seed(42)  # Set the seed for reproducibility

# Simulated absorbance data: (Experiments, Time Points, Wavelengths)
absorbance_data = np.random.rand(3, 4, 5)  # Shape (3, 4, 5)

print("Original Shape:", absorbance_data.shape)  # (3,4,5)
print(absorbance_data)  # Will always generate the same random values

Original Shape: (3, 4, 5)
[[[0.37454012 0.95071431 0.73199394 0.59865848 0.15601864]
  [0.15599452 0.05808361 0.86617615 0.60111501 0.70807258]
  [0.02058449 0.96990985 0.83244264 0.21233911 0.18182497]
  [0.18340451 0.30424224 0.52475643 0.43194502 0.29122914]]

 [[0.61185289 0.13949386 0.29214465 0.36636184 0.45606998]
  [0.78517596 0.19967378 0.51423444 0.59241457 0.04645041]
  [0.60754485 0.17052412 0.06505159 0.94888554 0.96563203]
  [0.80839735 0.30461377 0.09767211 0.68423303 0.44015249]]

 [[0.12203823 0.49517691 0.03438852 0.9093204  0.25877998]
  [0.66252228 0.31171108 0.52006802 0.54671028 0.18485446]
  [0.96958463 0.77513282 0.93949894 0.89482735 0.59789998]
  [0.92187424 0.0884925  0.19598286 0.04522729 0.32533033]]]

# Transpose: (Experiments, Time Points, Wavelengths) → (Wavelengths, Experiments, Time Points)
transposed_data = absorbance_data.transpose(2, 0, 1)

print("New Shape:", transposed_data.shape)  # Expected output: (5, 3, 4)
print(transposed_data)

New Shape: (5, 3, 4)
[[[0.37454012 0.15599452 0.02058449 0.18340451]
  [0.61185289 0.78517596 0.60754485 0.80839735]
  [0.12203823 0.66252228 0.96958463 0.92187424]]

 [[0.95071431 0.05808361 0.96990985 0.30424224]
  [0.13949386 0.19967378 0.17052412 0.30461377]
  [0.49517691 0.31171108 0.77513282 0.0884925 ]]

 [[0.73199394 0.86617615 0.83244264 0.52475643]
  [0.29214465 0.51423444 0.06505159 0.09767211]
  [0.03438852 0.52006802 0.93949894 0.19598286]]

 [[0.59865848 0.60111501 0.21233911 0.43194502]
  [0.36636184 0.59241457 0.94888554 0.68423303]
  [0.9093204  0.54671028 0.89482735 0.04522729]]

 [[0.15601864 0.70807258 0.18182497 0.29122914]
  [0.45606998 0.04645041 0.96563203 0.44015249]
  [0.25877998 0.18485446 0.59789998 0.32533033]]]

4.7: Merging Arrays#

Functions like np.concatenate(), np.vstack(), np.hstack(), and np.dstack() always create a new array. They do not modify the original arrays but instead return a new one that needs to be saved to a variable.

np.vstack()#

  • Adds arrays as new rows (along axis 0).

  • Requires matching number of columns.

Example: Combining Molecular Property Data Imagine we have two datasets:

  • Dataset 1: Molar masses of three molecules.

  • Dataset 2: Molar masses of three other molecules

import numpy as np

# Molecular masses (g/mol)
mass_data = np.array([[18.015],  # Water
                      [44.01],   # CO2
                      [32.00]])  # O2

# Boiling points (°C)
boiling_data = np.array([[100],  # Water
                         [-78.5], # CO2
                         [-183]]) # O2

# Stack them vertically
merged_data = np.vstack((mass_data, boiling_data))

print(merged_data)

import numpy as np

# Molecular masses (g/mol)
mass1_data = np.array([[18.015],  # Water
                      [44.01],   # CO2
                      [32.00]])  # O2

# Molecular massess (g/mol)
mass2_data = np.array([[180.16],  # Aspirin
                         [151.16], # Acetaminophen
                         [206.28]]) # Ibuprofen

# Stack them vertically
merged_data = np.vstack((mass1_data, mass2_data))

print(merged_data)

[[ 18.015]
 [ 44.01 ]
 [ 32.   ]
 [180.16 ]
 [151.16 ]
 [206.28 ]]

np.hstack()#

  • Adds arrays as new columns (along axis 1).

  • Requires matching number of rows.

Example: Combining Molecular Property Data Imagine we have two datasets:

  • Dataset 1: Molecular masses of three molecules.

  • Dataset 2: Their boiling points.

import numpy as np

# Molecular masses (g/mol)
mass_data = np.array([[18.015],  # Water
                      [44.01],   # CO2
                      [32.00]])  # O2

# Boiling points (°C)
boiling_data = np.array([[100],  # Water
                         [-78.5], # CO2
                         [-183]]) # O2
# Stack them horizontally
merged_data = np.hstack((mass_data, boiling_data))

import numpy as np

# Molecular masses (g/mol)
mass_data = np.array([[18.015],  # Water
                      [44.01],   # CO2
                      [32.00]])  # O2

# Boiling points (°C)
boiling_data = np.array([[100],  # Water
                         [-78.5], # CO2
                         [-183]]) # O2

# Stack them horizontally
merged_data = np.hstack((mass_data, boiling_data))

print(merged_data)

[[  18.015  100.   ]
 [  44.01   -78.5  ]
 [  32.    -183.   ]]

np.column_stack()#

  • Works like hstack(), but is specifically designed for 1D arrays.

Example: Pairing Element Symbols with Atomic Weights

# Element symbols
elements = np.array(['H', 'O', 'C'])

# Atomic masses
atomic_masses = np.array([1.008, 16.00, 12.01])

# Combine into a structured array
merged_data = np.column_stack((elements, atomic_masses))

print(merged_data)

[['H' '1.008']
 ['O' '16.0']
 ['C' '12.01']]

np.dstack( )#

  • only works on 1 and 2D arrays

  • Results in 3d arrays

Stacking 1D arrays#

import numpy as np

a = np.array([1, 2, 3])  # Shape (3,)
b = np.array([4, 5, 6])  # Shape (3,)

stacked = np.dstack((a, b))

print("Stacked shape:", stacked.shape)  # (1, 3, 2)
print(stacked)

Stacked shape: (1, 3, 2)
[[[1 4]
  [2 5]
  [3 6]]]

Stacking 2D arrays#

a = np.array([[1, 2], [3, 4]])  # Shape (2,2)
b = np.array([[5, 6], [7, 8]])  # Shape (2,2)

stacked = np.dstack((a, b))

print("Stacked shape:", stacked.shape)  # (2, 2, 2)
print(stacked)

Stacked shape: (2, 2, 2)
[[[1 5]
  [2 6]]

 [[3 7]
  [4 8]]]

np.stack()#

For higher order arrays you need np.stack()

import numpy as np

np.random.seed(42)  # Set the seed for reproducibility

# Define common wavelength range (same for all experiments)
wavelengths = np.linspace(400, 700, 5)  # 5 wavelengths from 400 to 700 nm

# Define common time scale (to enable stacking)
common_time = np.linspace(0, 100, 6)  # 6 time points from 0s to 100s

# Simulate absorbance data (random values for illustration)
exp1 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp2 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp3 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)

print("Shape of a single experiment dataset:", exp1.shape)  # (6, 5, 1)
# Stack experiments along a new axis (creating a 4D array)
spectroscopy_data = np.stack((exp1, exp2, exp3), axis=0)

print("Shape of stacked spectroscopy data:", spectroscopy_data.shape)  # (3,6,5,1)

Shape of a single experiment dataset: (6, 5, 1)
Shape of stacked spectroscopy data: (3, 6, 5, 1)

import numpy as np
import matplotlib.pyplot as plt

# Set seed for reproducibility
np.random.seed(42)

# Define common wavelength range (same for all experiments)
wavelengths = np.linspace(400, 700, 5)  # 5 wavelengths from 400 to 700 nm

# Define common time scale (to enable stacking)
common_time = np.linspace(0, 100, 6)  # 6 time points from 0s to 100s

# Simulate absorbance data (random values for illustration)
exp1 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp2 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp3 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)

# Stack experiments along a new axis (creating a 4D array)
spectroscopy_data = np.stack((exp1, exp2, exp3), axis=0)

# Function to plot absorbance over time for a specific wavelength across all experiments
def plot_absorbance_at_wavelength(target_wavelength):
    """
    Plots absorbance vs time for a specific wavelength across all experiments.
    
    Parameters:
    target_wavelength (float): The wavelength to extract absorbance values for.
    """
    num_experiments = spectroscopy_data.shape[0]  # Number of experiments

    # Find the closest wavelength index in the wavelength array
    wavelength_idx = np.argmin(np.abs(wavelengths - target_wavelength))

    # Define experiment labels for the legend
    experiment_labels = [f'Experiment {i+1}' for i in range(num_experiments)]
    
    # Set up a color cycle for experiments
    colors = ['b', 'g', 'r']

    # Create figure
    plt.figure(figsize=(7, 5))

    for exp_idx in range(num_experiments):
        absorbance_values = spectroscopy_data[exp_idx, :, wavelength_idx, 0]  # Extract absorbance data

        plt.plot(common_time, absorbance_values, marker='o', linestyle='-', color=colors[exp_idx], label=experiment_labels[exp_idx])

    plt.title(f'Absorbance at {target_wavelength} nm')
    plt.xlabel('Time (s)')
    plt.ylabel('Absorbance')
    plt.legend()
    plt.grid(True)

    plt.show()

# Plot absorbance at 620 nm across all experiments
plot_absorbance_at_wavelength(620)
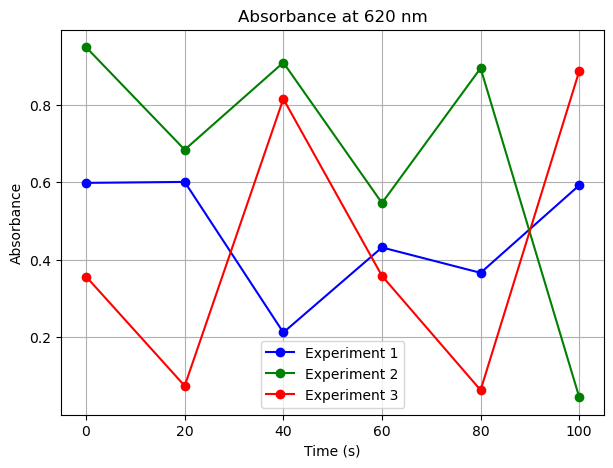
../../_images/28808e231106b64d44e28ec7c0250f9d6f93426e148861ce6527c0621d85a837.png

np.concatenate()#

In the above we had three experiments with the dimensions (6,5,1). We then added a fourth dimension usig np.stack() so that all three experiments are in the same array with the dimensions (3,6,5,1). We can use np.concatenate() to add a fourth experiment to the fourth dimension, giving a 4D array of shape (4,6,5,1).

# Set seed for reproducibility
np.random.seed(42)


# Simulate a new experiment (exp4) with the same shape as previous experiments
exp4 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)

# Use np.concatenate() to merge exp4 along axis=0 (experiment axis)
updated_spectroscopy_data = np.concatenate((spectroscopy_data, np.expand_dims(exp4, axis=0)), axis=0)

# Print the new shape to confirm
print("Updated 4D array shape:", updated_spectroscopy_data.shape)  # Expected: (4,6,5,1)

Updated 4D array shape: (4, 6, 5, 1)

import numpy as np
import matplotlib.pyplot as plt

# Set seed for reproducibility
np.random.seed(42)

# Define common wavelength range (same for all experiments)
wavelengths = np.linspace(400, 700, 5)  # 5 wavelengths from 400 to 700 nm

# Define common time scale (to enable stacking)
common_time = np.linspace(0, 100, 6)  # 6 time points from 0s to 100s

# Simulate absorbance data (random values for illustration)
exp1 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp2 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)
exp3 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)

# Stack experiments along a new axis (creating a 4D array)
spectroscopy_data = np.stack((exp1, exp2, exp3), axis=0)

# Simulate a new experiment (exp4) with the same shape as previous experiments
exp4 = np.random.rand(len(common_time), len(wavelengths), 1)  # Shape (6,5,1)

# Use np.concatenate() to merge exp4 along axis=0 (experiment axis)
updated_spectroscopy_data = np.concatenate((spectroscopy_data, np.expand_dims(exp4, axis=0)), axis=0)

# Function to plot absorbance at different times for all experiments
def plot_absorbance_at_times(times_to_plot):
    """
    Plots absorbance vs wavelength at selected time points for all experiments.
    
    Parameters:
    times_to_plot (list): List of time indices to plot.
    """
    num_experiments = updated_spectroscopy_data.shape[0]  # Number of experiments
    
    # Define experiment labels for the legend
    experiment_labels = [f'Experiment {i+1}' for i in range(num_experiments)]
    
    # Use the correct Matplotlib colormap approach
    cmap = plt.colormaps.get_cmap('tab10')  # Updated approach
    colors = [cmap(i % 10) for i in range(num_experiments)]  # Ensures correct color mapping

    # Create subplots for each selected time point
    fig, axes = plt.subplots(1, len(times_to_plot), figsize=(5 * len(times_to_plot), 5), sharey=True)

    if len(times_to_plot) == 1:
        axes = [axes]  # Ensure axes is iterable for a single plot

    for ax, time_idx in zip(axes, times_to_plot):
        for exp_idx in range(num_experiments):
            absorbance_values = updated_spectroscopy_data[exp_idx, time_idx, :, 0]  # Extract absorbance data

            ax.plot(wavelengths, absorbance_values, marker='o', linestyle='-', color=colors[exp_idx], label=experiment_labels[exp_idx])

        ax.set_title(f'Time = {common_time[time_idx]:.1f}s')
        ax.set_xlabel('Wavelength (nm)')
        ax.set_ylabel('Absorbance')
        ax.legend()
        ax.grid(True)

    plt.tight_layout()
    plt.show()

# Example: Plot absorbance at selected time points (Modify as needed)
plot_absorbance_at_times([0, 2, 5])  # Plot at first, middle, and last time points
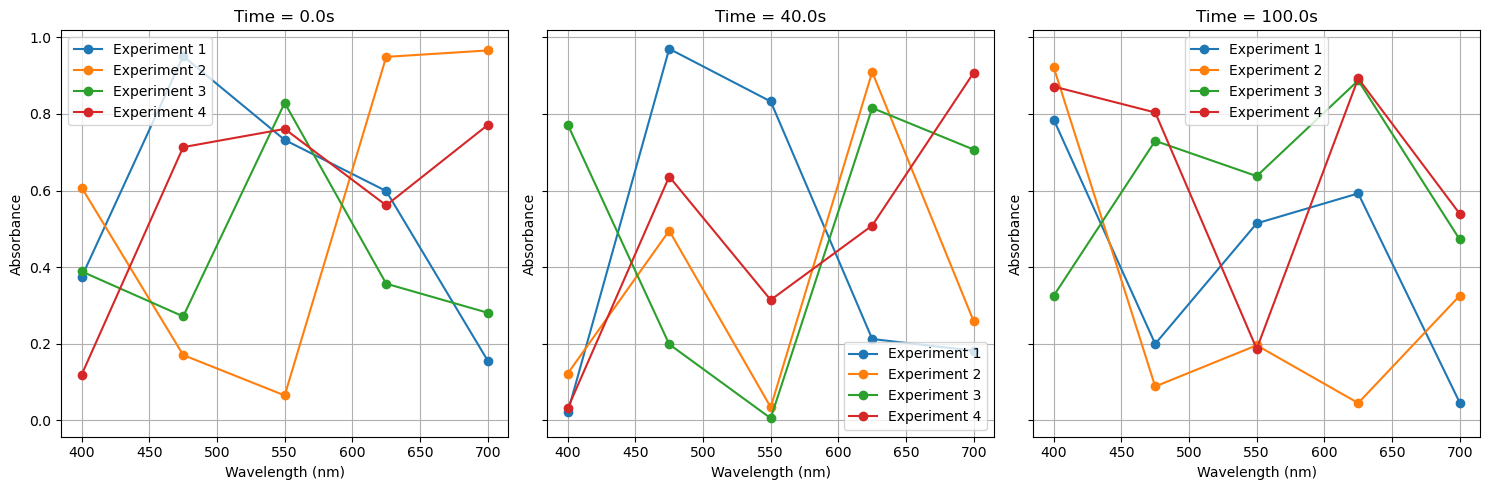
../../_images/7e38459db4d73ca6f9571dce774723872f43bbdb98388aae56675c68acd12803.png

4.8: Vectorization and Broadcasting Arrays#

Vectorization#

Because of the way arrays are stored in memory you can do operations on every element within an array without having to go through a loop. If the arrays have identical shapes this is called vectorization, and this is much faster than using loops.

In the following code we have two 1D arrays with 3 elements each, one containing the numbers of carbon, hydrogen and oxygen in a molecule, and the second the molar mass of carbon, hydrogen and oxygen. Two calculate the molar mass we simply multiply the two arrays by each other.

elements = np.array(['C', 'H', 'O'])
counts = np.array([6, 12, 6])

atomic_weights_np = np.array([12.01, 1.008, 16.00])  # Order matches elements

mass_matrix = atomic_weights_np * counts
print(mass_matrix)

total_mass = np.sum(atomic_weights_np * counts)
print(total_mass)  # 180.156 g/mol

What happens is

  • Index 0: 6 * 12.01 = 72.06

  • Index 1: 12 * 1.008

  • Index 2: 6 * 16.00 And this is much faster than looping.

elements = np.array(['C', 'H', 'O'])
counts = np.array([6, 12, 6])

atomic_weights_np = np.array([12.01, 1.008, 16.00])  # Order matches elements
mass_matrix = atomic_weights_np * counts
print(mass_matrix)

total_mass = np.sum(atomic_weights_np * counts)
print(total_mass)  # 180.156 g/mol

[72.06  12.096 96.   ]
180.156

Broadcasting#

If the shapes do not match Numpy Broadcasts from the array with the smaller dimensions to the larger by expanding the smaller one to fit the size of the larger.

Scalar math on arrays#

\[\begin{split} \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \end{array} \right] \times \left[ \begin{array}{c} 2 \end{array} \right]= ? \end{split}\]

becomes $\( \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \end{array} \right] \times \left[ \begin{array}{cc} 2 & 2 \\ 2 & 2 \end{array} \right]= \left[ \begin{array}{cc} 4 & 8 \\ 12 & 16 \end{array} \right] \)$



a = np.array([[2,4], [6,8]])
b = np.array([2]) 
a * b

array([[ 4,  8],
       [12, 16]])
\[\begin{split} \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \end{array} \right] \times \left[ \begin{array}{cc} 4 & 8 \end{array} \right]= ? \end{split}\]

becomes $\( \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \end{array} \right] \times \left[ \begin{array}{cc} 4 & 8 \\ 4 & 8 \end{array} \right]= \left[ \begin{array}{cc} 8 & 32 \\ 24 & 48 \end{array} \right] \)$

a = np.array([[2,4], [6,8]])
b = np.array([4,8])
a * b

array([[ 8, 32],
       [24, 64]])

4.9 Array io (saving arrays)#

You can save an array as a binary file (*.npy) or a binary compressed file (*.npz)

Save/Load a NumPy array#

import numpy as np

arr = np.array([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
np.save("data.npy", arr)  # Saves as binary file

loaded_arr = np.load("data.npy")
print(loaded_arr)

import numpy as np
import os

sandbox_dir = os.path.expanduser("~/sandbox/")
ndarray_npy_sbpath = os.path.join(sandbox_dir, "data.npy")

# Ensure the ~/sandbox/ directory exists
os.makedirs(sandbox_dir, exist_ok=True)

arr = np.array([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
np.save(ndarray_npy_sbpath, arr)  # Saves as binary file
print(arr)

[[1. 2. 3.]
 [4. 5. 6.]]

loaded_arr = np.load(ndarray_npy_sbpath)
print(loaded_arr)

[[1. 2. 3.]
 [4. 5. 6.]]

Save/Load multiple arrays#

np.savez("data.npz", arr1=arr, arr2=np.arange(10))

data = np.load("data.npz")
print(data["arr1"])  # Retrieve first array
print(data["arr2"])  # Retrieve second array

import numpy as np
import os

sandbox_dir = os.path.expanduser("~/sandbox/")
ndarray_npz_sbpath = os.path.join(sandbox_dir, "data.npz")

# Ensure the ~/sandbox/ directory exists
os.makedirs(sandbox_dir, exist_ok=True)

np.savez(ndarray_npz_sbpath, arr1=np.arange(1,25).reshape(6,4), arr2=np.arange(10))

data_files = np.load(ndarray_npz_sbpath)
print(data_files["arr1"])  # Retrieve first array
print(data_files["arr2"])  # Retrieve second array

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]
 [21 22 23 24]]
[0 1 2 3 4 5 6 7 8 9]

5. Random Number Generation#

The random submodule allows for a variety of random number generations. It is a very powerful tool for creating datasets to test programs with, and these can be tailored to fit different distributions.

Compare Random module with np.random submodule#

import random

# Define isotopes and their natural abundance
isotopes = ["Cl-35", "Cl-37"]
weights = [0.75, 0.25]  # Probabilities based on natural abundance

# Generate 1000 random selections
random_sample = random.choices(isotopes, weights=weights, k=1000)

# Count occurrences
cl_35_count = random_sample.count("Cl-35")
cl_37_count = random_sample.count("Cl-37")

# Print results
print(f"Using random module:")
print(f"Cl-35: {cl_35_count}, Cl-37: {cl_37_count}")

Using random module:
Cl-35: 764, Cl-37: 236

# Numpy random Submodule
import numpy as np

# Define isotopes and their probabilities
isotopes = np.array(["Cl-35", "Cl-37"])
probabilities = [0.75, 0.25]

# Generate 1000 random selections using NumPy
np_sample = np.random.choice(isotopes, size=1000, p=probabilities)

# Count occurrences using NumPy
unique, counts = np.unique(np_sample, return_counts=True)
isotope_counts = dict(zip(unique, counts))

# Print results
print("\nUsing numpy.random:")
print(f"Cl-35: {isotope_counts['Cl-35']}, Cl-37: {isotope_counts['Cl-37']}")

Using numpy.random:
Cl-35: 749, Cl-37: 251

Comparing the time we see that the numpy.random.choice is an order of magnitude faster than random.choices

import time

# Using random module
start = time.time()
random_sample = random.choices(isotopes, weights=weights, k=1_000_000)
end = time.time()
print(f"random.choices() time: {end - start:.5f} seconds")

# Using numpy.random
start = time.time()
np_sample = np.random.choice(isotopes, size=1_000_000, p=probabilities)
end = time.time()
print(f"numpy.random.choice() time: {end - start:.5f} seconds")

random.choices() time: 0.29654 seconds
numpy.random.choice() time: 0.03485 seconds

Functions and Methods in numpy.random#

Name

Type

Description

random_sample()

Function

Generates random floats uniformly distributed in [0.0, 1.0).

rand()

Function

Generates random values in a given shape from a uniform distribution over [0, 1).

randint()

Function

Returns random integers from a specified range.

choice()

Function

Randomly selects elements from a given 1D array or list.

uniform()

Function

Generates random floats uniformly distributed between specified low and high values.

normal()

Function

Draws samples from a normal (Gaussian) distribution with specified mean and standard deviation.

standard_normal()

Function

Returns samples from a standard normal distribution (mean=0, std=1).

seed()

Method

Sets the seed for reproducibility of random number generation.

RandomState()

Class/Method

Creates a container for managing random number generation with its own state.

default_rng()

Method

Returns a new instance of the default random number generator introduced in NumPy 1.17.

integers()

Method

Generates random integers over a specified range (replacement for randint in newer versions).

shuffle()

Method

Shuffles the elements of an array in place.

permutation()

Method

Returns a permuted sequence or array without modifying the input.

beta()

Function

Draws samples from a Beta distribution.

binomial()

Function

Draws samples from a Binomial distribution.

poisson()

Function

Draws samples from a Poisson distribution.

exponential()

Function

Draws samples from an exponential distribution.

gamma()

Function

Draws samples from a Gamma distribution.

geometric()

Function

Draws samples from a geometric distribution.

np.random.seed()#

A random.seed allows you to generate the same random values when you rerun the code.

  • Allows reproducible data sets

  • Global - affects all subsequent random generation calls within a program unless another seed is set.

  • Works with random functions like np.random.rand() and np.random.int()

import numpy as np

# Set the seed
np.random.seed(42)

# Generate 10 random numbers to the hundredth place
random_numbers = np.round(np.random.rand(10), 2)
print(random_numbers)

[0.37 0.95 0.73 0.6  0.16 0.16 0.06 0.87 0.6  0.71]

np.random.default_rng()#

This allows you to create an independent (non global random instance). Note, the second time you call it the numbers are different because you have advanced through the seed iteration, and you need to reset the seed to start over.

import numpy as np

# First approach: The RNG advances
rng1 = np.random.default_rng(42) # seed is 42
rng2 = np.random.default_rng(99) # seed is 99

print("First call - RNG 1:", rng1.random(3))  # Advances
print("First call - RNG 2:", rng2.random(3))  # Advances

print("Second call - RNG 1:", rng1.random(3))  # Different numbers!
print("Second call - RNG 2:", rng2.random(3))  # Different numbers!

# Reset the generators
rng1 = np.random.default_rng(42)  # Reinitialize
rng2 = np.random.default_rng(99)  # Reinitialize

print("Reset and first call again - RNG 1:", rng1.random(3))  # Same as first call!
print("Reset and first call again - RNG 2:", rng2.random(3))  # Same as first call!

First call - RNG 1: [0.77395605 0.43887844 0.85859792]
First call - RNG 2: [0.50603067 0.56509163 0.51191596]
Second call - RNG 1: [0.69736803 0.09417735 0.97562235]
Second call - RNG 2: [0.97218637 0.61490314 0.5682835 ]
Reset and first call again - RNG 1: [0.77395605 0.43887844 0.85859792]
Reset and first call again - RNG 2: [0.50603067 0.56509163 0.51191596]

Uniform Distribution#

import numpy as np
import matplotlib.pyplot as plt

# Create an independent RNG
rng = np.random.default_rng(42)

# Generate 1000 random numbers from uniform distribution
uniform_data = rng.uniform(size=1000)


# Create a histogram plot
plt.figure(figsize=(10, 6))

# Plot uniform distribution histogram
plt.hist(uniform_data, bins=30, alpha=0.5, color='blue', label="uniform()")



# Labels and title
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.title("Histogram of uniform data)")
plt.legend()
plt.grid(True)

# Show the histogram
plt.show()
../../_images/c8e2791815bf2dd15cd3b259ab7b8f78a8c13543821ec14b488122958869e285.png 
import numpy as np
import matplotlib.pyplot as plt

# Create an independent RNG
rng = np.random.default_rng(42)

# Generate 1000 random numbers from uniform distribution
standard_normal_data = rng.standard_normal(size=1000)


# Create a histogram plot
plt.figure(figsize=(10, 6))

# Plot uniform distribution histogram
plt.hist(standard_normal_data, bins=30, alpha=0.5, color='blue', label="uniform()")



# Labels and title
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.title("Histogram of standard normal data)")
plt.legend()
plt.grid(True)

# Show the histogram
plt.show()
../../_images/2c937a38965190514387993f080a0d571fde323a2d509cbafbabc7d42d1bb6e8.png

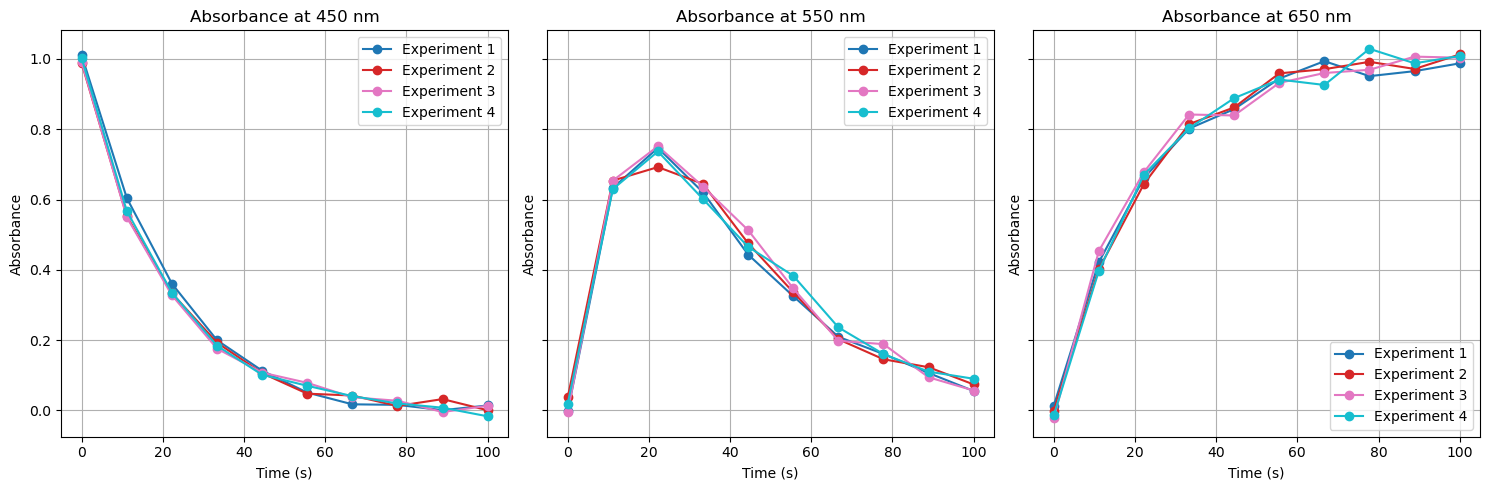
Inserting noise into an equation.

import numpy as np
import matplotlib.pyplot as plt

# Set seed for reproducibility
np.random.seed(42)

# Define wavelengths for R, I, and P
wavelengths = np.array([450, 550, 650])  # nm

# Define common time scale (10 points over 100s)
common_time = np.linspace(0, 100, 10)  

# Define the number of experiments
num_experiments = 4  

# Function to simulate reaction kinetics: R → I → P
def reaction_profiles(time):
    """
    Simulates reaction kinetics:
    - R (Reactant) decays exponentially.
    - I (Intermediate) forms, then decays as P forms.
    - P (Product) forms as I decays.
    """
    R = np.exp(-0.05 * time)  # Exponential decay for R
    I = (time * np.exp(-0.05 * time)) / 10  # Intermediate formation & decay
    P = (1 - np.exp(-0.05 * time))  # Product formation

    return np.array([R, I, P]).T  # Transpose to match (time, species)

# Initialize a NumPy array to store absorbance data (4D array)
# Shape: (Experiments, Time, Wavelengths, 1)
absorbance_data = np.zeros((num_experiments, len(common_time), len(wavelengths), 1))

# Generate data for each experiment
for exp_idx in range(num_experiments):
    reaction_data = reaction_profiles(common_time)  # Get kinetic profiles

    # Introduce slight experimental variations using a random factor
    noise = np.random.normal(0, 0.02, reaction_data.shape)  # Small noise added
    absorbance_data[exp_idx, :, :, 0] = reaction_data + noise  # Store data

# Function to plot absorbance vs time at selected wavelengths
def plot_absorbance_at_wavelengths():
    """
    Plots absorbance vs time for selected wavelengths (450nm, 550nm, 650nm),
    representing Reactant, Intermediate, and Product formation.
    """
    experiment_labels = [f'Experiment {i+1}' for i in range(num_experiments)]
    colors = plt.cm.tab10(np.linspace(0, 1, num_experiments))  # Assign colors

    # Create subplots for each wavelength
    fig, axes = plt.subplots(1, len(wavelengths), figsize=(15, 5), sharey=True)

    for ax, wavelength_idx in zip(axes, range(len(wavelengths))):
        for exp_idx in range(num_experiments):
            absorbance_values = absorbance_data[exp_idx, :, wavelength_idx, 0]  # Extract data

            ax.plot(common_time, absorbance_values, marker='o', linestyle='-',
                    color=colors[exp_idx], label=experiment_labels[exp_idx])

        ax.set_title(f'Absorbance at {wavelengths[wavelength_idx]} nm')
        ax.set_xlabel('Time (s)')
        ax.set_ylabel('Absorbance')
        ax.legend()
        ax.grid(True)

    plt.tight_layout()
    plt.show()

# Plot absorbance at 450nm, 550nm, and 650nm
plot_absorbance_at_wavelengths()
../../_images/cd5c0752e3e1d0e5055ad1d8934b578bdb1c847e518fbd272d1a9b14cedb1761.png 
# Show data of second experiment
absorbance_data[1, :, :, 0]

array([[ 9.87965868e-01,  3.70455637e-02, -2.69944495e-04],
       [ 5.52599202e-01,  6.53954699e-01,  4.01829706e-01],
       [ 3.33370260e-01,  6.92346570e-01,  6.44243291e-01],
       [ 1.92812828e-01,  6.44354674e-01,  8.14551763e-01],
       [ 1.06055058e-01,  4.75613585e-01,  8.62061537e-01],
       [ 4.77796399e-02,  3.36212358e-01,  9.58965921e-01],
       [ 4.25463591e-02,  2.02565819e-01,  9.70807686e-01],
       [ 1.27664301e-02,  1.45657704e-01,  9.91765450e-01],
       [ 3.23636189e-02,  1.23013411e-01,  9.71472021e-01],
       [ 5.53699482e-04,  7.40047386e-02,  1.01277296e+00]])

# Show first four temporal measurements of third experiment
absorbance_data[2, 0:4, :, 0]

array([[ 0.99041652, -0.00371318, -0.0221267 ],
       [ 0.54982929,  0.65375432,  0.45337138],
       [ 0.32775279,  0.75161063,  0.67803973],
       [ 0.17597321,  0.63681325,  0.84188513]])

# Show the decay of the first experiment
absorbance_data[0, :, 0, 0]

array([1.00993428e+00, 6.04214018e-01, 3.60777244e-01, 1.99726804e-01,
       1.13207269e-01, 5.09307734e-02, 1.75135118e-02, 1.59525497e-02,
       8.55973967e-04, 1.42519074e-02])

#Find the values of the reactant and product when the intermediate is max.
print(absorbance_data.shape)
# Find the time index where Intermediate (I) is max for each experiment
max_I_indices = np.argmax(absorbance_data[:, :, 1, 0], axis=1)  # I at index 1 (550 nm)

# Extract corresponding R (450 nm) and P (650 nm) values
R_at_max_I = absorbance_data[np.arange(num_experiments), max_I_indices, 0, 0]  # R at 450nm
P_at_max_I = absorbance_data[np.arange(num_experiments), max_I_indices, 2, 0]  # P at 650nm

# Print results
for exp_idx in range(num_experiments):
    time_at_max_I = common_time[max_I_indices[exp_idx]]
    print(f"Experiment {exp_idx+1}:")
    print(f"  Time at max I: {time_at_max_I:.2f} s")
    print(f"  R (450nm) at max I: {R_at_max_I[exp_idx]:.3f}")
    print(f"  P (650nm) at max I: {P_at_max_I[exp_idx]:.3f}\n")

(4, 10, 3, 1)
Experiment 1:
  Time at max I: 22.22 s
  R (450nm) at max I: 0.361
  P (650nm) at max I: 0.661

Experiment 2:
  Time at max I: 22.22 s
  R (450nm) at max I: 0.333
  P (650nm) at max I: 0.644

Experiment 3:
  Time at max I: 22.22 s
  R (450nm) at max I: 0.328
  P (650nm) at max I: 0.678

Experiment 4:
  Time at max I: 22.22 s
  R (450nm) at max I: 0.335
  P (650nm) at max I: 0.671

6. Masks#

A mask is a way of filtering data based on a condition.

  • Instead of looping through a dataset and using if statements, we can use a Boolean mask to select specific values efficiently.

In NumPy, masks are frequently used for filtering arrays.

.nonzero()#

nonzero() returns the indices of elements that are non-zero (or True for boolean arrays). For a 1D array, it returns a tuple containing a single array of indices. For multi-dimensional arrays, it returns a tuple of arrays, one for each dimension.

import numpy as np

# Define the array
darray = np.array([3, 1, 8, -8, 2, 8])

# Create a boolean mask where values equal to 8 are True
mask = (darray == 8)
print("Mask:", mask)  # [False False  True False False  True]

# Use nonzero() to find indices where mask is True
print("nonzero() result:", mask.nonzero())  # returns a tuple of arrays
print("Extracted indices:", mask.nonzero()[0])  # extract the first array from the tuple

# Separate analysis of the types
nonzero_result = mask.nonzero()
print("nonzero_result:", nonzero_result)  # (array([2, 5]),)
print("type of nonzero_result:", type(nonzero_result))  # <class 'tuple'>
print("type of nonzero_result[0]:", type(nonzero_result[0]))  # <class 'numpy.ndarray'>

Mask: [False False  True False False  True]
nonzero() result: (array([2, 5]),)
Extracted indices: [2 5]
nonzero_result: (array([2, 5]),)
type of nonzero_result: <class 'tuple'>
type of nonzero_result[0]: <class 'numpy.ndarray'>

Example: Finding Temperatures Above a Threshold

import numpy as np

# Temperature readings in °C
temperatures = np.array([20, 25, 30, 15, 10, 35, 40])

# Mask for temperatures above 25°C
high_temps = temperatures > 25  
print(high_temps)  # [False False  True False False  True  True]

# Use the mask to filter values
filtered_temps = temperatures[high_temps]
print(filtered_temps)  # [30 35 40]

Why is this useful?

  • Instead of writing a loop with an if statement, we filter data in a single operation.

  • Faster execution for large datasets.

  • Useful for analyzing experimental datasets (e.g., selecting only high-energy molecules).

Why NumPy Handles True Boolean Masks#

  1. Boolean Indexing

    • NumPy allows direct indexing using a Boolean array (mask), which is not possible with standard lists.

    • Example:

      import numpy as np
arr = np.array([10, 15, 20, 25])
mask = arr > 15  # [False, False, True, True]
print(arr[mask])  # Output: [20 25]

      • This directly filters elements based on the mask.

      • Lists don’t support this; you’d need a list comprehension instead.

  2. Performance Optimization

    • NumPy operates at C-level speed under the hood, making Boolean masks much faster than loops or comprehensions in pure Python.

  3. Logical Operations on Masks

    • You can combine conditions efficiently using NumPy’s element-wise operations:

      mask = (arr > 10) & (arr < 25)  # Using bitwise AND for multiple conditions
print(arr[mask])

      • Standard lists require multiple loops or conditions inside a comprehension.

import numpy as np

# Temperature readings in °C
temperatures = np.array([20, 25, 30, 15, 10, 35, 40])

# Mask for temperatures above 25°C
high_temps = temperatures > 25  
print(high_temps)  # [False False  True False False  True  True]

# Use the mask to filter values
filtered_temps = temperatures[high_temps]
print(filtered_temps)  # [30 35 40]

[False False  True False False  True  True]
[30 35 40]

random mask (the following will print between 0 and 10 values that were generated as true

atomic_numbers = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
random_mask = np.random.randint(0, 2, size=10, dtype=bool)  # Random 0/1 mask
selected_data = atomic_numbers[random_mask]  
print(selected_data)  # Random subset of elements

[2 4 5 6 7]

.where#

import numpy as np
data = np.array([3,1,8,-8,2,8])
mask = np.where(data == 8, np.arange(np.size(data)), 0)
print(mask)

[0 0 2 0 0 5]

8. Missing Data#

IEEE NaN (Not a Number)#

  • IEEE standard for floating point arithmetic.

  • Represents the absence of a valid numerical value in floating point systems

Using Boolean Masks for NaN#

import numpy as np

arr = np.array([1.0, 2.0, np.nan, 4.0, 5.0])
print(arr)

[ 1.  2. nan  4.  5.]

nan_mask = np.isnan(arr)
print(nan_mask)

[False False  True False False]

nan_mask = ~np.isnan(arr)
print(nan_mask)

[ True  True False  True  True]

The ~ is the Bitwise NOT operator and inverts the boolean mask

  • ~ inverts the Boolean mask:

    • True → False

    • False → True

arr_no_nan = arr[~np.isnan(arr)]
print(arr_no_nan)

[1. 2. 4. 5.]

9. NumPy Statistics#

Function

Description

Example

np.mean()

Calculates the arithmetic mean

np.mean([1, 2, 3, 4, 5])

np.median()

Calculates the median (middle value)

np.median([1, 2, 3, 4, 5])

np.std()

Calculates the standard deviation

np.std([1, 2, 3, 4, 5])

np.var()

Calculates the variance

np.var([1, 2, 3, 4, 5])

np.min()

Finds the minimum value

np.min([1, 2, 3, 4, 5])

np.max()

Finds the maximum value

np.max([1, 2, 3, 4, 5])

np.percentile()

Calculates the qth percentile

np.percentile([1, 2, 3, 4, 5], 50)

np.sum()

Calculates the sum of all elements

np.sum([1, 2, 3, 4, 5])

np.prod()

Calculates the product of all elements

np.prod([1, 2, 3, 4, 5])

np.cumsum()

Calculates the cumulative sum

np.cumsum([1, 2, 3, 4, 5])

np.cumprod()

Calculates the cumulative product

np.cumprod([1, 2, 3, 4, 5])

np.argmin()

Returns the index of the minimum value

np.argmin([3, 1, 2, 4, 5])

np.argmax()

Returns the index of the maximum value

np.argmax([3, 1, 2, 4, 5])

np.ptp()

Range of values (max - min)

np.ptp([1, 2, 3, 4, 5])

10. Numpy NaN Statistics#

Function

Description

Example

np.nanmax(arr)

Maximum value, ignoring NaNs

np.nanmax([1, 2, np.nan, 4])

np.nanmin(arr)

Minimum value, ignoring NaNs

np.nanmin([1, np.nan, 3, 4])

np.nanmean(arr)

Arithmetic mean, ignoring NaNs

np.nanmean([1, 2, np.nan, 4])

np.nanmedian(arr)

Median value, ignoring NaNs

np.nanmedian([1, np.nan, 3, 4])

np.nansum(arr)

Sum of elements, ignoring NaNs

np.nansum([1, 2, np.nan, 4])

np.nanstd(arr)

Standard deviation, ignoring NaNs

np.nanstd([1, 2, np.nan, 4])

np.nanvar(arr)

Variance, ignoring NaNs

np.nanvar([1, 2, np.nan, 4])

np.nanprod(arr)

Product of elements, ignoring NaNs

np.nanprod([1, 2, np.nan, 4])

np.nancumsum(arr)

Cumulative sum, ignoring NaNs

np.nancumsum([1, 2, np.nan, 4])

np.nancumprod(arr)

Cumulative product, ignoring NaNs

np.nancumprod([1, 2, np.nan, 4])

np.nanpercentile(arr, q)

Compute percentiles, ignoring NaNs

np.nanpercentile([1, np.nan, 3, 4], 50)

np.nanquantile(arr, q)

Compute quantiles, ignoring NaNs

np.nanquantile([1, np.nan, 3, 4], 0.5)

12. Other Numpy DataTypes#

besides ndarray there are several other datatypes provided by the numpy package

9.1: Structured arrays (np.array)#

  • Allows defining heterogeneous data types .

  • Example:

# Define a structured dtype with multiple fields
dtype = [('name', 'U10'), ('mass', 'f4'), ('charge', 'i4')]

# Create a structured array with different field types
structured_arr = np.array([
    ('Electron', 9.11e-31, -1),
    ('Proton', 1.67e-27, +1)
], dtype=dtype)

print(structured_arr)
print(type(structured_arr))  # <class 'numpy.ndarray'>


# Define a structured dtype with multiple fields
dtype = [('name', 'U10'), ('mass', 'f4'), ('charge', 'i4')]

# Create a structured array with different field types
structured_arr = np.array([
    ('Electron', 9.11e-31, -1),
    ('Proton', 1.67e-27, +1)
], dtype=dtype)

print(structured_arr)
print(type(structured_arr))  # <class 'numpy.ndarray'>

[('Electron', 9.11e-31, -1) ('Proton', 1.67e-27,  1)]
<class 'numpy.ndarray'>

How Are Structured Arrays Different from Regular ndarrays?#

Feature

Regular ndarray

Structured Array (np.ndarray with dtype)

Data Type

Homogeneous (dtype is the same for all elements)

Heterogeneous (dtype varies across fields)

Row Access

Indexed by number (arr[i])

Indexed by number (arr[i])

Column Access

Not supported natively

Accessed by field names (arr['column'])

Resemblance to DataFrames?

No

Yes (similar to structured tables)

9.2: Masked arrays (np.ma.array)#

  • A subclass of ndarray that allows elements to be masked (ignored) in computations.

  • Useful for handling missing or invalid data without affecting computations.

  • Example:

    import numpy as np
a = np.ma.array([1, 2, 3, 4], mask=[False, True, False, False])
print(a.mean())  # Ignores masked elements

9.3: Record Arrays (np.recarray)#

A variation of structured arrays with attribute-style access. Example: rec = np.rec.array([(‘Hydrogen’, 1.008), (‘Oxygen’, 16.00)], dtype=[(‘element’, ‘U10’), (‘mass’, ‘f4’)]) print(rec.element) # Access column as an attribute

Acknowledgements#

This content was developed with assistance from Perplexity AI and Chat GPT. Multiple queries were made during the Fall 2024 and the Spring 2025.

Contents