4. MatPlotLib

4. MatPlotLib#

1. Introduction to Pyplot#

Matplotlib (https://matplotlib.org/) is a comprehensive library for creating static, animated, and interactive visualizations in Python. It’s one of the most popular plotting libraries in the Python ecosystem. Matplotlib is built on Numpy and so we often import them together

To install matplotlib (be sure to be in proper virtual environment)

conda install -c conda-forge matplotlib

There are two basic ways to use MatPlotlib, either through the PyPlot submodule or through an object oriented approach where programs use the objects within MatPlotlib.

Pyplot vs. Object-Oriented Approach:#

Feature

Pyplot (Stateful)

Object-Oriented (OO)

Figure creation

plt.figure() (optional, implicit)

fig, ax = plt.subplots()

Plotting

plt.plot(...)

ax.plot(...)

Labels, title, etc.

plt.xlabel(), plt.title(), etc.

ax.set_xlabel(), ax.set_title(), etc.

Layout adjustment

plt.tight_layout()

fig.tight_layout()

Use of figure/axes objects

No

Yes (explicit fig, ax)

In this class we will use matplotlib.pyplot approach and import it into our Jupyter notebooks through the following command

To import

import matplotlib.pyplot as plt
import numpy as np

Pyplot (often imported as plt) is a module within Matplotlib that provides a simple, MATLAB-like interface for plotting. It’s designed to make common plotting tasks easy and accessible, especially for users familiar with MATLAB’s plotting commands.

1.1: Pyplot classes#

Pyplot itself is not a class, but rather a module that provides a MATLAB-like interface to Matplotlib. However, it interacts with and creates instances of several important classes within the Matplotlib ecosystem. Here are some key points:

  1. Figure Class: Pyplot creates and manages instances of the Figure class. The Figure class is the top-level container for all plot elements[1].

  2. Axes Class: When you create plots using pyplot functions, you’re often working with instances of the Axes class, which represent individual plotting areas within a figure.

  3. Canvas Class: The FigureCanvas is indeed a class, and it’s crucial in Matplotlib’s architecture. It’s the object that actually does the drawing of the figure.

  4. FigureManager Class: This class is responsible for managing the interaction between the Figure and the backend.

2. Generating a Figure#

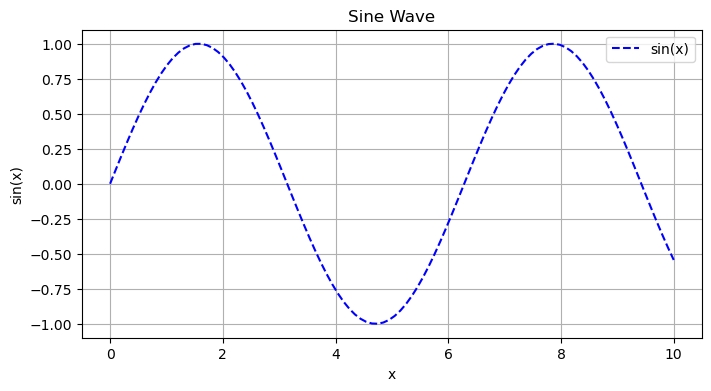
Each plt.fig() statement in the following code block creates an independent figure state, and the subsequent plotting commands only apply to that figure.

import matplotlib.pyplot as plt
import numpy as np

# Data for Plot 1
x1 = np.linspace(0, 10, 100)
y1 = np.sin(x1)

# First Figure
plt.figure(figsize=(8, 4))
plt.plot(x1, y1, label='sin(x)', color='blue', linestyle='--')
plt.title("Sine Wave")
plt.xlabel("x")
plt.ylabel("sin(x)")
plt.legend()
plt.grid(True)
plt.show()

# Data for Plot 2
x2 = np.linspace(0, 5, 100)
y2 = np.exp(-x2)

# Second Figure
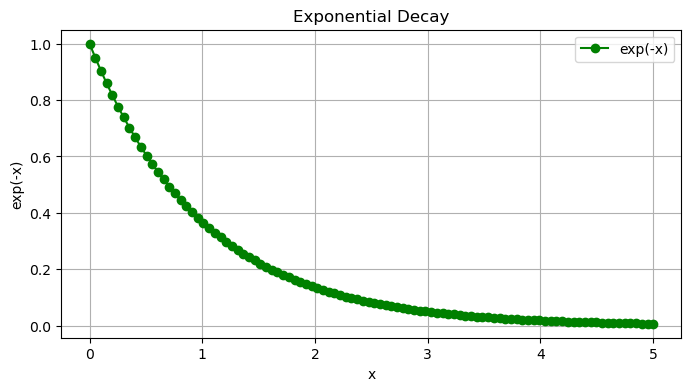
plt.figure(figsize=(8, 4))
plt.plot(x2, y2, label='exp(-x)', color='green', marker='o')
plt.title("Exponential Decay")
plt.xlabel("x")
plt.ylabel("exp(-x)")
plt.legend()
plt.grid(True)
plt.show()
../../_images/87c941c1944e716c7aa1637db3dbe841338752e10621b2813c02419a25ba6801.png ../../_images/bad050df91348420d085ec2c2adbf91752d9c72cce0a4324ee3dc48f3956dc90.png

2.1 Understanding plt.functions in the figure#

Lets look at the following block of code

plt.figure(figsize=(8, 4))
plt.plot(x1, y1, label='sin(x)', color='blue')
plt.title("Sine Wave")
plt.xlabel("x")
plt.ylabel("sin(x)")
plt.legend()
plt.grid(True)
plt.show()

Function

Purpose

Key Parameters

plt.figure()

Create a new figure (canvas)

figsize=(width, height) in inches

plt.plot()

Plot data as a line

x, y, label, color, linestyle, marker

plt.title()

Add plot title

label, optional: fontsize, loc

plt.xlabel()

Label x-axis

label, optional: fontsize, labelpad

plt.ylabel()

Label y-axis

label, optional: fontsize, labelpad

plt.legend()

Display legend box

optional: loc, fontsize, title, frameon

plt.grid()

Add grid lines

True/False, optional: axis, color, linestyle

plt.show()

Render and display plot

None

3. Pyplot Functions#

Method

Description

plot()

Creates a line or scatter plot

scatter()

Creates a scatter plot

bar()

Creates a bar plot

hist()

Creates a histogram

boxplot()

Creates a box and whisker plot

imshow()

Displays an image on a 2D regular raster

contour()

Draws contour lines

contourf()

Draws filled contours

quiver()

Plots a 2D field of arrows

pie()

Creates a pie chart

errorbar()

Plots y versus x as lines and/or markers with attached error bars

subplot()

Adds a subplot to the current figure

figure()

Creates a new figure or activates an existing figure

title()

Sets a title for the current axes

xlabel()

Sets a label for the x-axis

ylabel()

Sets a label for the y-axis

legend()

Places a legend on the axes

grid()

Configures the grid lines

xlim()

Gets or sets the x limits of the current axes

ylim()

Gets or sets the y limits of the current axes

savefig()

Saves the current figure

show()

Displays all open figures

close()

Closes a figure window

colorbar()

Adds a colorbar to a plot

clim()

Sets the color limits of the current image

text()

Adds text to the axes

annotate()

Annotates a point with text

3.1 pyplot.plot()#

plplot.plot arguments#

Argument

Description

x

The horizontal coordinates of the data points. Optional if y is given as a 2D array.

y

The vertical coordinates of the data points.

fmt

A format string that specifies the color, marker, and line style. Optional.

color

The color of the line or markers. Can be a string or RGB tuple.

linestyle

The style of the line. Examples: ‘-’, ‘–’, ‘:’, ‘-.’

linewidth

The width of the line in points.

marker

The style of markers to use. Examples: ‘o’, ‘s’, ‘^’, ‘D’

markersize

The size of markers in points.

label

A string that will be used in the legend for this line.

alpha

The transparency of the line/markers (0.0 to 1.0).

data

An object with labelled data, allowing use of string identifiers for x and y.

scalex, scaley

Booleans indicating whether to autoscale x and y axes. Default is True.

4. Plots from Equations#

Radial Wavefunction for Hydrogen-like Atoms#

The radial part of the wavefunction is given by:

\[ R_{n,\ell}(r) = N_{n\ell} \cdot e^{- \rho / 2} \cdot \rho^{\ell} \cdot L_{n-\ell-1}^{2\ell + 1}(\rho) \]

where

\[ \rho = \frac{2r}{n a_0} \]

and the normalization factor \( N_{nl}\) is:

\[ N_{n\ell} = \sqrt{\left(\frac{2}{n a_0}\right)^3 \cdot \frac{(n - \ell - 1)!}{2n (n + \ell)!}} \]

The radial probability density is:

\[ P(r) = r^2 \cdot |R_{n,\ell}(r)|^2 \]

where ( a_0 ) is the Bohr radius.

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import genlaguerre
from scipy.constants import physical_constants
import math

# Constants
a0 = physical_constants['Bohr radius'][0]  # Bohr radius in meters

# Define the radial wave function for hydrogen-like atoms
def radial_wavefunction(n, l, r):
    """Computes the radial wavefunction R_{n,l}(r) for hydrogen-like atoms."""
    rho = 2 * r / (n * a0)
    norm_factor = np.sqrt((2 / (n * a0))**3 * math.factorial(n - l - 1) / (2 * n * math.factorial(n + l)))
    #norm_factor = np.sqrt((2 / (n * a0))**3 * np.math.factorial(n - l - 1) / (2 * n * np.math.factorial(n + l)))
    laguerre_poly = genlaguerre(n - l - 1, 2 * l + 1)
    radial_part = np.exp(-rho / 2) * rho**l * laguerre_poly(rho)
    return norm_factor * radial_part

# Define radial probability density P(r) = r^2 * |R_{n,l}(r)|^2
def radial_probability(n, l, r):
    R = radial_wavefunction(n, l, r)
    return r**2 * R**2


# Radial range
r_values = np.linspace(0, 25 * a0, 500)  # Up to 10 Bohr radii

# Compute radial probability densities
prob_1s = radial_probability(1, 0, r_values)
prob_2s = radial_probability(2, 0, r_values)
prob_3s = radial_probability(3, 0, r_values)
prob_2p = radial_probability(2, 1, r_values)
# Plot
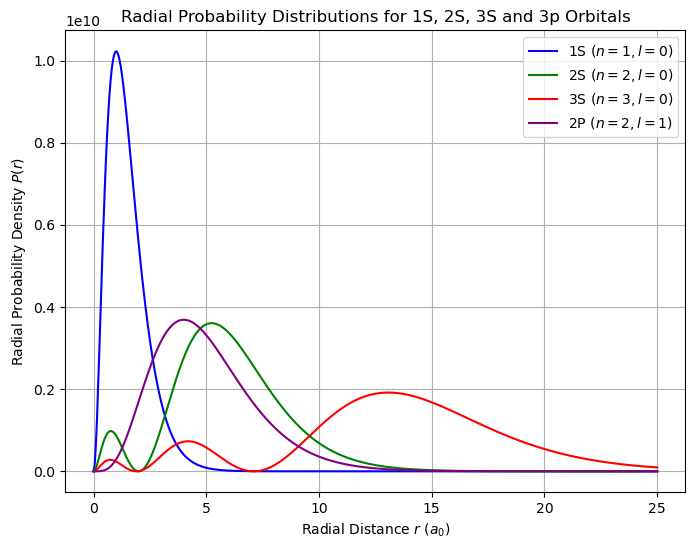
plt.figure(figsize=(8, 6))
plt.plot(r_values / a0, prob_1s, label=r'1S ($n=1, l=0$)', color='b')
plt.plot(r_values / a0, prob_2s, label=r'2S ($n=2, l=0$)', color='g')
plt.plot(r_values / a0, prob_3s, label=r'3S ($n=3, l=0$)', color='r')
plt.plot(r_values / a0, prob_2p, label=r'2P ($n=2, l=1$)', color='purple')

# Labels and title
plt.xlabel(r'Radial Distance $r$ ($a_0$)')
plt.ylabel(r'Radial Probability Density $P(r)$')
plt.title('Radial Probability Distributions for 1S, 2S, 3S and 3p Orbitals')
plt.legend()
plt.grid(True)

# Show plot
plt.show()
../../_images/0ddec18b41aaa6373651600e03a9f619b489304c7233777556e5e2ae3fd3b0c1.png

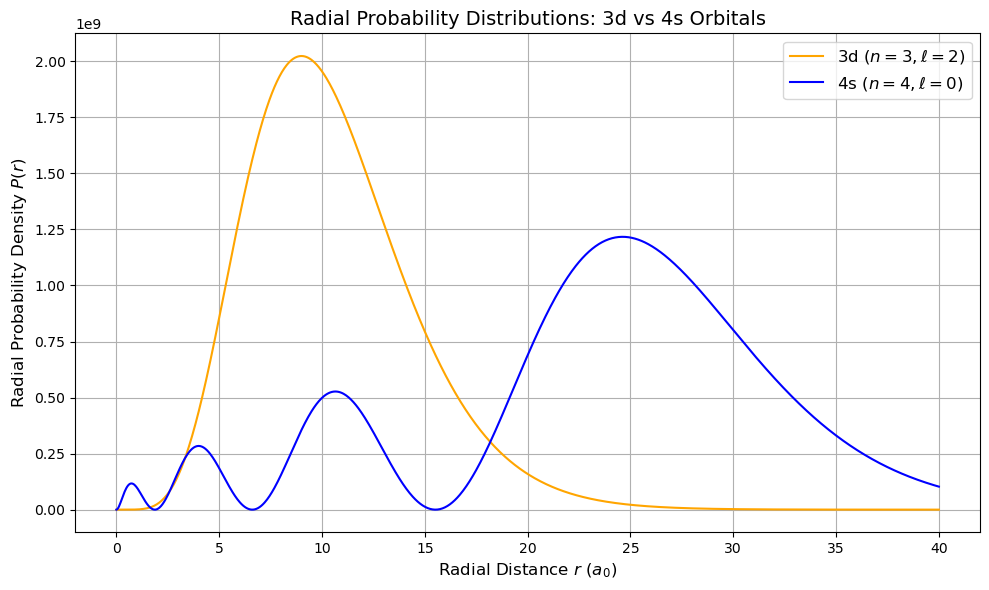
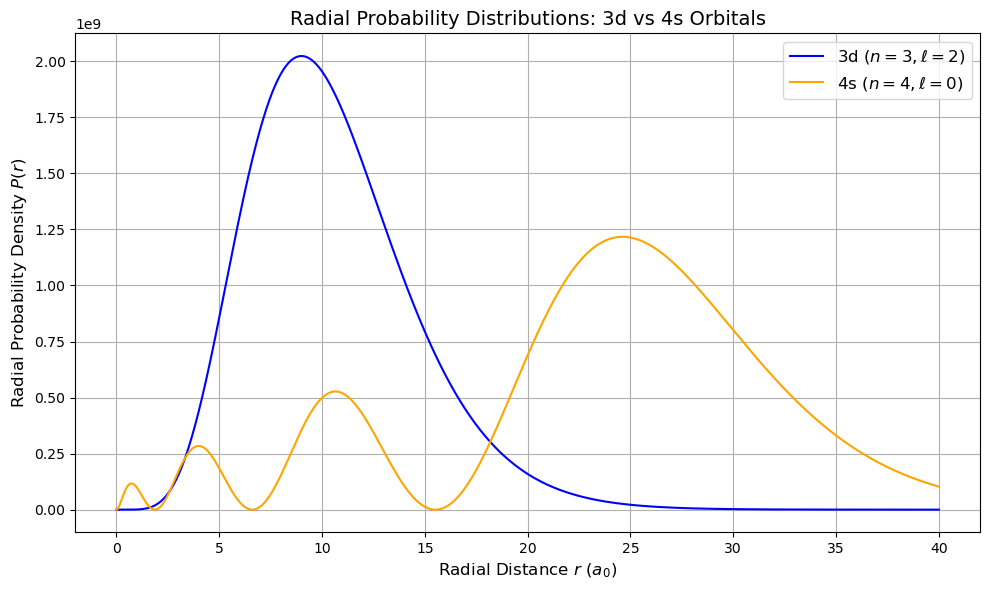
Radial Probability Densities: 3d vs 4s Orbitals#

The radial probability density is defined as:

\[ P(r) = r^2 \cdot |R_{n,\ell}(r)|^2 \]

where \( R_{n,l}(r)\) is the radial wavefunction for hydrogen-like atoms.

  • 3d orbital: n = 3, l = 2

  • 4s orbital: n = 4, l = 0

The 4s orbital shows significant penetration closer to the nucleus and also extends farther out than the 3d orbital. This behavior explains trends in electron configurations and chemical reactivity in the periodic table.

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import genlaguerre
from scipy.constants import physical_constants
import math

# Constants
a0 = physical_constants['Bohr radius'][0]  # Bohr radius in meters

# Radial wavefunction R_{n,l}(r)
def radial_wavefunction(n, l, r):
    rho = 2 * r / (n * a0)
    norm_factor = np.sqrt((2 / (n * a0))**3 * math.factorial(n - l - 1) / (2 * n * math.factorial(n + l)))
    laguerre_poly = genlaguerre(n - l - 1, 2 * l + 1)
    radial_part = np.exp(-rho / 2) * rho**l * laguerre_poly(rho)
    return norm_factor * radial_part

# Radial probability density P(r) = r^2 * |R_{n,l}(r)|^2
def radial_probability(n, l, r):
    R = radial_wavefunction(n, l, r)
    return r**2 * R**2

# Radial distances
r_values = np.linspace(0, 40 * a0, 1000)  # Up to 20 Bohr radii for better comparison

# Compute radial probability densities
prob_3d = radial_probability(3, 2, r_values)
prob_4s = radial_probability(4, 0, r_values)

# Plot
plt.figure(figsize=(10, 6))
plt.plot(r_values / a0, prob_3d, label=r'3d ($n=3, \ell=2$)', color='orange')
plt.plot(r_values / a0, prob_4s, label=r'4s ($n=4, \ell=0$)', color='blue')
plt.xlabel(r'Radial Distance $r$ ($a_0$)', fontsize=12)
plt.ylabel(r'Radial Probability Density $P(r)$', fontsize=12)
plt.title('Radial Probability Distributions: 3d vs 4s Orbitals', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.tight_layout()
plt.show()
../../_images/3ddf13fae3149886f0e93bfd65b7e1b341034ba0bc214a5c399f87974dde1752.png 
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import genlaguerre
from scipy.constants import physical_constants
import math  # Use math.factorial for scalars

# Constants
a0 = physical_constants['Bohr radius'][0]  # Bohr radius in meters

# Radial wavefunction R_{n,l}(r)
def radial_wavefunction(n, l, r):
    rho = 2 * r / (n * a0)
    norm_factor = np.sqrt((2 / (n * a0))**3 * math.factorial(n - l - 1) / (2 * n * math.factorial(n + l)))
    laguerre_poly = genlaguerre(n - l - 1, 2 * l + 1)
    radial_part = np.exp(-rho / 2) * rho**l * laguerre_poly(rho)
    return norm_factor * radial_part

# Radial probability density P(r) = r^2 * |R_{n,l}(r)|^2
def radial_probability(n, l, r):
    R = radial_wavefunction(n, l, r)
    return r**2 * R**2

# Radial distance values (0 to 40 Bohr radii)
r_values = np.linspace(0, 40 * a0, 1000)

# Compute probability densities for 3d and 4s
prob_3d = radial_probability(3, 2, r_values)
prob_4s = radial_probability(4, 0, r_values)

# Plot
plt.figure(figsize=(10, 6))
plt.plot(r_values / a0, prob_3d, label=r'3d ($n=3, \ell=2$)', color='blue')
plt.plot(r_values / a0, prob_4s, label=r'4s ($n=4, \ell=0$)', color='orange')

# Labels, title, legend
plt.xlabel(r'Radial Distance $r$ ($a_0$)', fontsize=12)
plt.ylabel(r'Radial Probability Density $P(r)$', fontsize=12)
plt.title('Radial Probability Distributions: 3d vs 4s Orbitals', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.tight_layout()
plt.show()
../../_images/900365dd57fb4e93b4d2c9ffd488a20066c6f3a393464e797e6ce6397bac821b.png

5. Plots from periodic table#

# Use the directory structure from Workbook 4
import pandas as pd
import os
base_data_dir = os.path.expanduser("~/data")  # Parent directory
pubchem_data_dir = os.path.join(base_data_dir, "pubchem_data")  # Subdirectory for PubChem
os.makedirs(pubchem_data_dir, exist_ok=True)  # Ensure directories exist
periodictable_csv_datapath = os.path.join(pubchem_data_dir, "PubChemElements_all.csv")
df_periodictable = pd.read_csv(periodictable_csv_datapath, index_col=1)
df_periodictable.head()
AtomicNumber Name AtomicMass CPKHexColor ElectronConfiguration Electronegativity AtomicRadius IonizationEnergy ElectronAffinity OxidationStates StandardState MeltingPoint BoilingPoint Density GroupBlock YearDiscovered
Symbol
H 1 Hydrogen 1.008000 FFFFFF 1s1 2.20 120.0 13.598 0.754 +1, -1 Gas 13.81 20.28 0.000090 Nonmetal 1766
He 2 Helium 4.002600 D9FFFF 1s2 NaN 140.0 24.587 NaN 0 Gas 0.95 4.22 0.000179 Noble gas 1868
Li 3 Lithium 7.000000 CC80FF [He]2s1 0.98 182.0 5.392 0.618 +1 Solid 453.65 1615.00 0.534000 Alkali metal 1817
Be 4 Beryllium 9.012183 C2FF00 [He]2s2 1.57 153.0 9.323 NaN +2 Solid 1560.00 2744.00 1.850000 Alkaline earth metal 1798
B 5 Boron 10.810000 FFB5B5 [He]2s2 2p1 2.04 192.0 8.298 0.277 +3 Solid 2348.00 4273.00 2.370000 Metalloid 1808 
#df_periodictable=df_periodictable.set_index("Symbol")
df_periodictable.head()
AtomicNumber Name AtomicMass CPKHexColor ElectronConfiguration Electronegativity AtomicRadius IonizationEnergy ElectronAffinity OxidationStates StandardState MeltingPoint BoilingPoint Density GroupBlock YearDiscovered
Symbol
H 1 Hydrogen 1.008000 FFFFFF 1s1 2.20 120.0 13.598 0.754 +1, -1 Gas 13.81 20.28 0.000090 Nonmetal 1766
He 2 Helium 4.002600 D9FFFF 1s2 NaN 140.0 24.587 NaN 0 Gas 0.95 4.22 0.000179 Noble gas 1868
Li 3 Lithium 7.000000 CC80FF [He]2s1 0.98 182.0 5.392 0.618 +1 Solid 453.65 1615.00 0.534000 Alkali metal 1817
Be 4 Beryllium 9.012183 C2FF00 [He]2s2 1.57 153.0 9.323 NaN +2 Solid 1560.00 2744.00 1.850000 Alkaline earth metal 1798
B 5 Boron 10.810000 FFB5B5 [He]2s2 2p1 2.04 192.0 8.298 0.277 +3 Solid 2348.00 4273.00 2.370000 Metalloid 1808

Save DataFrame with symbols as index#

This sets the first column as the index

df_periodictable.to_csv("pubchem_periodic_table.csv", index=True)

my_df=pd.read_csv("pubchem_periodic_table.csv")
my_df.head()
Symbol AtomicNumber Name AtomicMass CPKHexColor ElectronConfiguration Electronegativity AtomicRadius IonizationEnergy ElectronAffinity OxidationStates StandardState MeltingPoint BoilingPoint Density GroupBlock YearDiscovered
0 H 1 Hydrogen 1.008000 FFFFFF 1s1 2.20 120.0 13.598 0.754 +1, -1 Gas 13.81 20.28 0.000090 Nonmetal 1766
1 He 2 Helium 4.002600 D9FFFF 1s2 NaN 140.0 24.587 NaN 0 Gas 0.95 4.22 0.000179 Noble gas 1868
2 Li 3 Lithium 7.000000 CC80FF [He]2s1 0.98 182.0 5.392 0.618 +1 Solid 453.65 1615.00 0.534000 Alkali metal 1817
3 Be 4 Beryllium 9.012183 C2FF00 [He]2s2 1.57 153.0 9.323 NaN +2 Solid 1560.00 2744.00 1.850000 Alkaline earth metal 1798
4 B 5 Boron 10.810000 FFB5B5 [He]2s2 2p1 2.04 192.0 8.298 0.277 +3 Solid 2348.00 4273.00 2.370000 Metalloid 1808 
#When we read the dataframe we can set the index_col to the first one
my_df=pd.read_csv("pubchem_periodic_table.csv", index_col=0)
my_df.head()
AtomicNumber Name AtomicMass CPKHexColor ElectronConfiguration Electronegativity AtomicRadius IonizationEnergy ElectronAffinity OxidationStates StandardState MeltingPoint BoilingPoint Density GroupBlock YearDiscovered
Symbol
H 1 Hydrogen 1.008000 FFFFFF 1s1 2.20 120.0 13.598 0.754 +1, -1 Gas 13.81 20.28 0.000090 Nonmetal 1766
He 2 Helium 4.002600 D9FFFF 1s2 NaN 140.0 24.587 NaN 0 Gas 0.95 4.22 0.000179 Noble gas 1868
Li 3 Lithium 7.000000 CC80FF [He]2s1 0.98 182.0 5.392 0.618 +1 Solid 453.65 1615.00 0.534000 Alkali metal 1817
Be 4 Beryllium 9.012183 C2FF00 [He]2s2 1.57 153.0 9.323 NaN +2 Solid 1560.00 2744.00 1.850000 Alkaline earth metal 1798
B 5 Boron 10.810000 FFB5B5 [He]2s2 2p1 2.04 192.0 8.298 0.277 +3 Solid 2348.00 4273.00 2.370000 Metalloid 1808 
df_periodictable.describe()
AtomicNumber AtomicMass Electronegativity AtomicRadius IonizationEnergy ElectronAffinity MeltingPoint BoilingPoint Density
count 118.000000 118.000000 95.000000 99.000000 102.000000 57.000000 103.000000 93.000000 96.000000
mean 59.500000 146.540281 1.732316 209.464646 7.997255 1.072140 1273.740553 2536.212473 7.608001
std 34.207699 89.768356 0.635187 38.569130 3.339066 0.879163 888.853859 1588.410919 5.878692
min 1.000000 1.008000 0.700000 120.000000 3.894000 0.079000 0.950000 4.220000 0.000090
25% 30.250000 66.480750 1.290000 187.000000 6.020500 0.470000 516.040000 1180.000000 2.572500
50% 59.500000 142.573830 1.620000 209.000000 6.960000 0.754000 1191.000000 2792.000000 7.072000
75% 88.750000 226.777165 2.170000 232.000000 8.998500 1.350000 1806.500000 3618.000000 10.275250
max 118.000000 295.216000 3.980000 348.000000 24.587000 3.617000 3823.000000 5869.000000 22.570000 
df_periodictable.info()

<class 'pandas.core.frame.DataFrame'>
Index: 118 entries, H to Og
Data columns (total 16 columns):
 #   Column                 Non-Null Count  Dtype  
---  ------                 --------------  -----  
 0   AtomicNumber           118 non-null    int64  
 1   Name                   118 non-null    object 
 2   AtomicMass             118 non-null    float64
 3   CPKHexColor            108 non-null    object 
 4   ElectronConfiguration  118 non-null    object 
 5   Electronegativity      95 non-null     float64
 6   AtomicRadius           99 non-null     float64
 7   IonizationEnergy       102 non-null    float64
 8   ElectronAffinity       57 non-null     float64
 9   OxidationStates        117 non-null    object 
 10  StandardState          118 non-null    object 
 11  MeltingPoint           103 non-null    float64
 12  BoilingPoint           93 non-null     float64
 13  Density                96 non-null     float64
 14  GroupBlock             118 non-null    object 
 15  YearDiscovered         118 non-null    object 
dtypes: float64(8), int64(1), object(7)
memory usage: 15.7+ KB

Lets start by making a list of the elements in the third period of the atomic table

third_period_atomic_numbers = list(range(11, 19))  # Na (11) to Ar (18)
print(third_period_atomic_numbers)

[11, 12, 13, 14, 15, 16, 17, 18]

Now lets convert their atomic numbers to the symbols, which is what the dataframe above uses for row labels

# Filter for third-period elements
third_period_df = df_periodictable[df_periodictable['AtomicNumber'].isin(third_period_atomic_numbers)]

# Sort by AtomicNumber for correct x-axis order
third_period_df = third_period_df.sort_values('AtomicNumber')

# Extract values for plotting
atomic_numbers = third_period_df['AtomicNumber'].values
ionization_energies = third_period_df['IonizationEnergy'].values
electronegativities = third_period_df['Electronegativity'].values
symbols = third_period_df.index.values  # This will be element symbols
print(f"atomic_numbers: {atomic_numbers} \n ionization energies: {ionization_energies} \n electronegativities: {electronegativities} \n symbols: {symbols}")

atomic_numbers: [11 12 13 14 15 16 17 18] 
 ionization energies: [ 5.139  7.646  5.986  8.152 10.487 10.36  12.968 15.76 ] 
 electronegativities: [0.93 1.31 1.61 1.9  2.19 2.58 3.16  nan] 
 symbols: ['Na' 'Mg' 'Al' 'Si' 'P' 'S' 'Cl' 'Ar']

import matplotlib.pyplot as plt

fig, ax1 = plt.subplots(figsize=(10, 6))

# Left y-axis: Ionization Energy
color1 = 'tab:blue'
ax1.set_xlabel('Atomic Number')
ax1.set_ylabel('Ionization Energy (eV)', color=color1)
ax1.plot(atomic_numbers, ionization_energies, marker='o', color=color1, label='Ionization Energy')
ax1.tick_params(axis='y', labelcolor=color1)

# X-ticks as element symbols
ax1.set_xticks(atomic_numbers)
ax1.set_xticklabels(symbols)

# Right y-axis: Electronegativity
ax2 = ax1.twinx()
color2 = 'tab:red'
ax2.set_ylabel('Electronegativity', color=color2)
ax2.plot(atomic_numbers, electronegativities, marker='s', linestyle='--', color=color2, label='Electronegativity')
ax2.tick_params(axis='y', labelcolor=color2)

# Title and layout
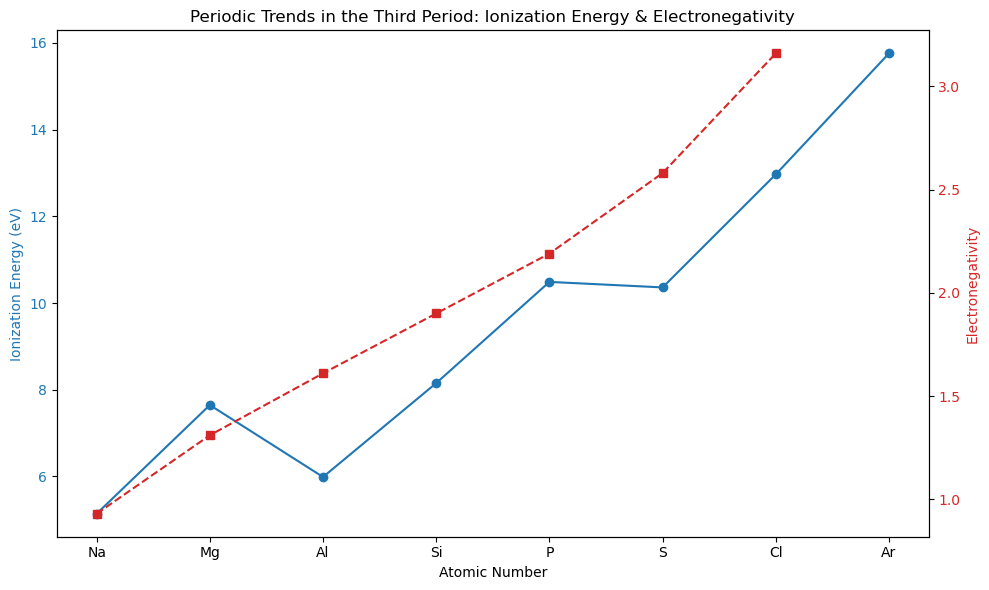
plt.title('Periodic Trends in the Third Period: Ionization Energy & Electronegativity')
fig.tight_layout()
plt.show()
../../_images/2882192884fbc3c73174cdd77d4e46991d832f8d0f5b0acfe6dbb722b042fd17.png

`

In Class activity#

alter the above code to work for the second row of the periodic table

Alter the above code to show the trends of atomic radius and atomic mass as you go across the fourth period

Periodic trend of electronegativity

import numpy as np
import matplotlib.pyplot as plt

# Sort by Atomic Number to maintain order
df_sorted = df_periodictable.sort_values('AtomicNumber')

# Extract data
atomic_numbers = df_sorted['AtomicNumber'].values
ionization_energies = df_sorted['IonizationEnergy'].values
electronegativities = df_sorted['Electronegativity'].values
symbols = df_sorted.index.values  # element symbols
print(f"atomic_numbers: {atomic_numbers}\n ionization energies: {ionization_energies}  \n symbols: {symbols}")

atomic_numbers: [  1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18
  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36
  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51  52  53  54
  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72
  73  74  75  76  77  78  79  80  81  82  83  84  85  86  87  88  89  90
  91  92  93  94  95  96  97  98  99 100 101 102 103 104 105 106 107 108
 109 110 111 112 113 114 115 116 117 118]
 ionization energies: [13.598 24.587  5.392  9.323  8.298 11.26  14.534 13.618 17.423 21.565
  5.139  7.646  5.986  8.152 10.487 10.36  12.968 15.76   4.341  6.113
  6.561  6.828  6.746  6.767  7.434  7.902  7.881  7.64   7.726  9.394
  5.999  7.9    9.815  9.752 11.814 14.     4.177  5.695  6.217  6.634
  6.759  7.092  7.28   7.361  7.459  8.337  7.576  8.994  5.786  7.344
  8.64   9.01  10.451 12.13   3.894  5.212  5.577  5.539  5.464  5.525
  5.55   5.644  5.67   6.15   5.864  5.939  6.022  6.108  6.184  6.254
  5.426  6.825  7.89   7.98   7.88   8.7    9.1    9.     9.226 10.438
  6.108  7.417  7.289  8.417  9.5   10.745  3.9    5.279  5.17   6.08
  5.89   6.194  6.266  6.06   5.993  6.02   6.23   6.3    6.42   6.5
  6.58   6.65     nan    nan    nan    nan    nan    nan    nan    nan
    nan    nan    nan    nan    nan    nan    nan    nan]  
 symbols: ['H' 'He' 'Li' 'Be' 'B' 'C' 'N' 'O' 'F' 'Ne' 'Na' 'Mg' 'Al' 'Si' 'P' 'S'
 'Cl' 'Ar' 'K' 'Ca' 'Sc' 'Ti' 'V' 'Cr' 'Mn' 'Fe' 'Co' 'Ni' 'Cu' 'Zn' 'Ga'
 'Ge' 'As' 'Se' 'Br' 'Kr' 'Rb' 'Sr' 'Y' 'Zr' 'Nb' 'Mo' 'Tc' 'Ru' 'Rh' 'Pd'
 'Ag' 'Cd' 'In' 'Sn' 'Sb' 'Te' 'I' 'Xe' 'Cs' 'Ba' 'La' 'Ce' 'Pr' 'Nd' 'Pm'
 'Sm' 'Eu' 'Gd' 'Tb' 'Dy' 'Ho' 'Er' 'Tm' 'Yb' 'Lu' 'Hf' 'Ta' 'W' 'Re' 'Os'
 'Ir' 'Pt' 'Au' 'Hg' 'Tl' 'Pb' 'Bi' 'Po' 'At' 'Rn' 'Fr' 'Ra' 'Ac' 'Th'
 'Pa' 'U' 'Np' 'Pu' 'Am' 'Cm' 'Bk' 'Cf' 'Es' 'Fm' 'Md' 'No' 'Lr' 'Rf' 'Db'
 'Sg' 'Bh' 'Hs' 'Mt' 'Ds' 'Rg' 'Cn' 'Nh' 'Fl' 'Mc' 'Lv' 'Ts' 'Og']

# Mask valid (non-NaN) entries
valid_mask = ~np.isnan(electronegativities)

fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(atomic_numbers[valid_mask], ionization_energies[valid_mask],
        marker='o', linestyle='-', color='teal')

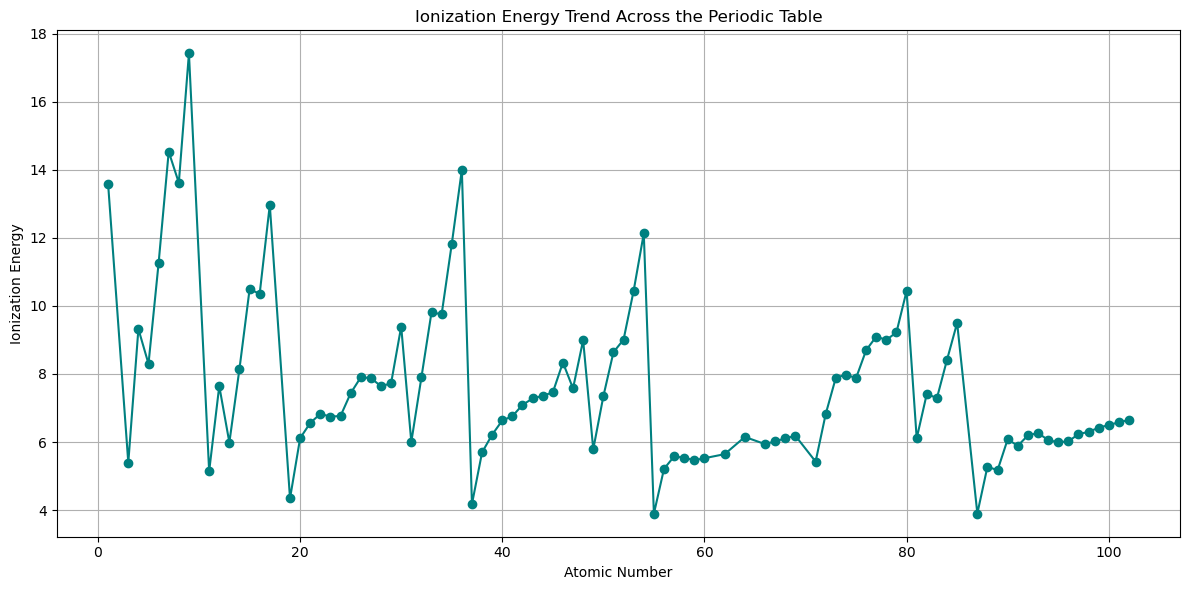
ax.set_title('Ionization Energy Trend Across the Periodic Table')
ax.set_xlabel('Atomic Number')
ax.set_ylabel('Ionization Energy')
ax.grid(True)

plt.tight_layout()
plt.show()
../../_images/1755063fc2a30dfd9b4e2f03860a2bf0065d2e509e9f268fba70604f0b6c0159.png 
# For categorical x-axis, skip NaN values and align arrays
valid_indices = np.where(valid_mask)[0]
valid_symbols = symbols[valid_mask]
valid_en = electronegativities[valid_mask]

fig, ax = plt.subplots(figsize=(16, 6))
ax.plot(valid_symbols, valid_en, marker='o', linestyle='-', color='purple')

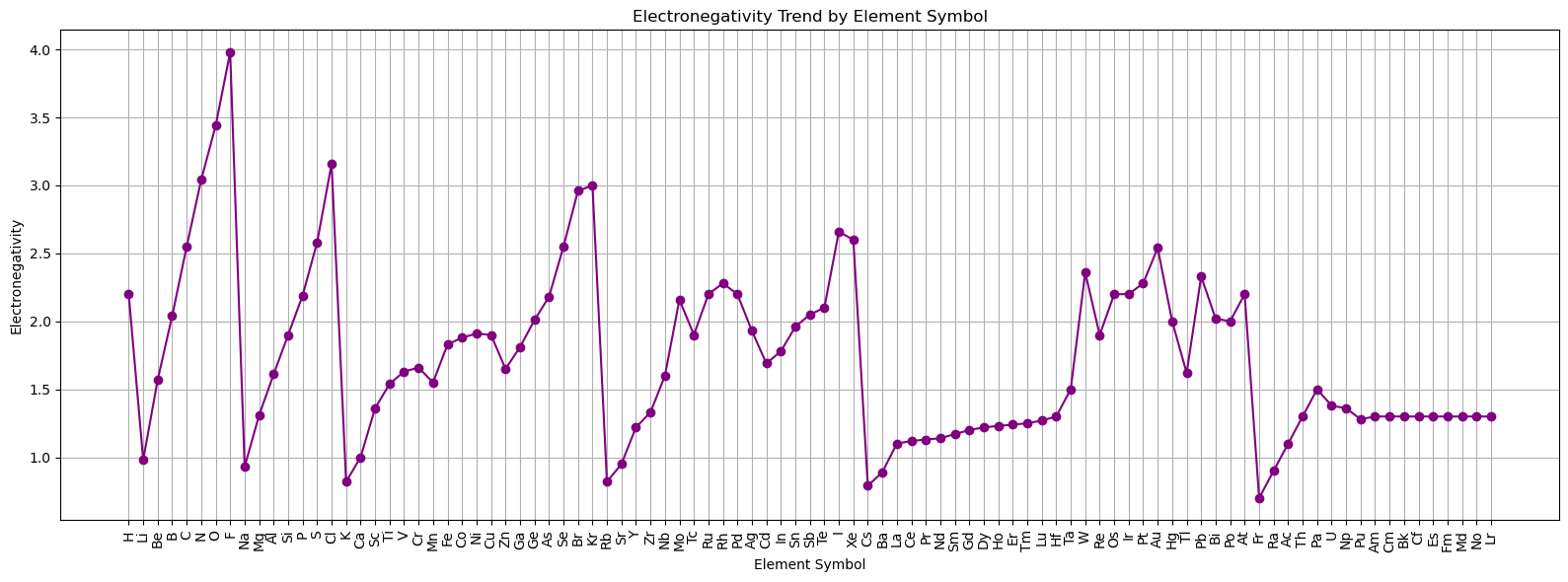
ax.set_title('Electronegativity Trend by Element Symbol')
ax.set_xlabel('Element Symbol')
ax.set_ylabel('Electronegativity')
ax.grid(True)

# Rotate x-tick labels for readability
plt.xticks(rotation=90)

plt.tight_layout()
plt.show()
../../_images/1630cc91ae7cfc64ecb20aa388ad3f39c5992d798a1df526ceb315a745c15f7a.png 
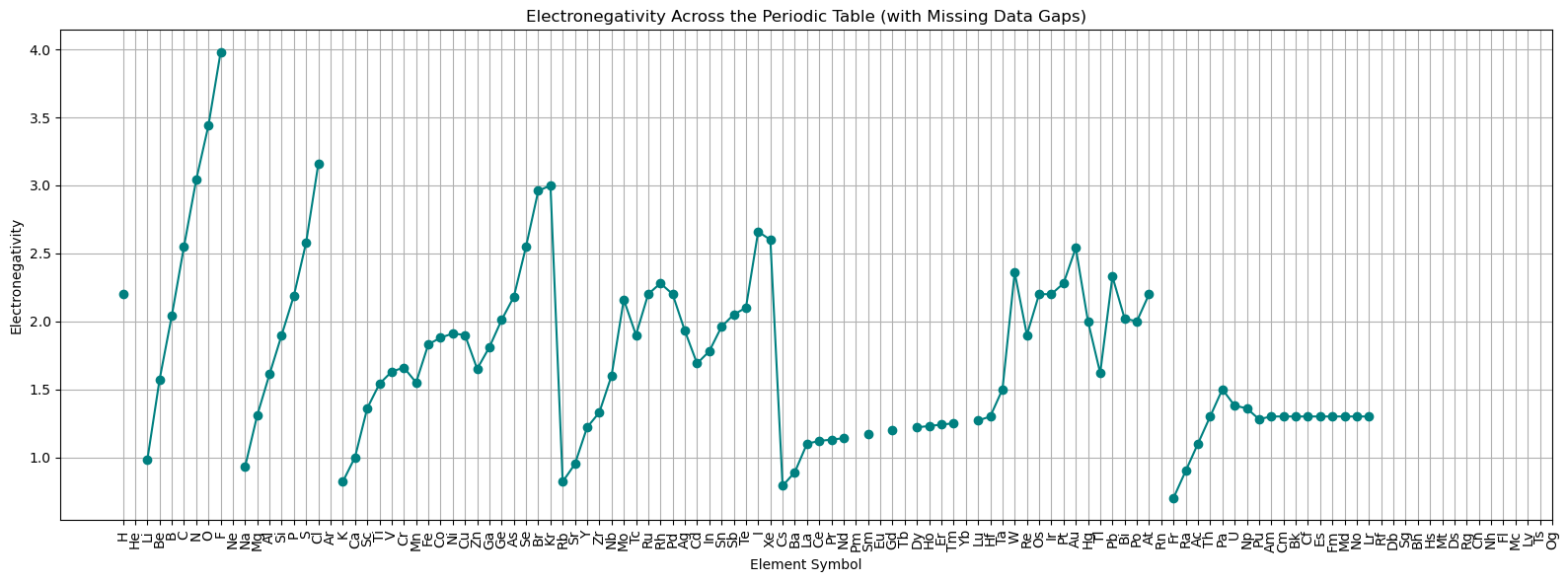
import numpy as np
import matplotlib.pyplot as plt

# Sort by AtomicNumber
df_sorted = df_periodictable.sort_values('AtomicNumber')

# Get all atomic numbers and symbols (x-axis)
atomic_numbers = df_sorted['AtomicNumber'].values
symbols = df_sorted.index.values  # element symbols as index

# Prepare Electronegativity data (with NaNs for missing values)
electronegativity = df_sorted['Electronegativity'].values

# Now plot with NaNs preserved
fig, ax = plt.subplots(figsize=(16, 6))

# Plot line: breaks at NaNs
ax.plot(atomic_numbers, electronegativity, linestyle='-', marker='o', color='teal')

# Set x-axis ticks and labels
ax.set_xticks(atomic_numbers)
ax.set_xticklabels(symbols, rotation=90)

# Labels and grid
ax.set_title('Electronegativity Across the Periodic Table (with Missing Data Gaps)')
ax.set_xlabel('Element Symbol')
ax.set_ylabel('Electronegativity')
ax.grid(True)

plt.tight_layout()
plt.show()
../../_images/f53a36bb9d78676cc93641a582518ed73ba37e072f3626bc66870544522199c7.png

Histograms vs. Bar Charts#

Feature

Histogram

Bar Plot

Data Type

Continuous/numeric (e.g., mass, radius)

Categorical (e.g., element groups)

X-Axis

Bins/ranges (e.g., 0–50, 50–100)

Categories (e.g., “Alkali”, “Noble Gas”)

Bar Width

No gaps between bars (adjacent bins)

Gaps between bars (separate categories)

Purpose

Shows distribution of values

Compares quantities between groups/categories

Example

Distribution of Atomic Radius values

Number of elements in each GroupBlock

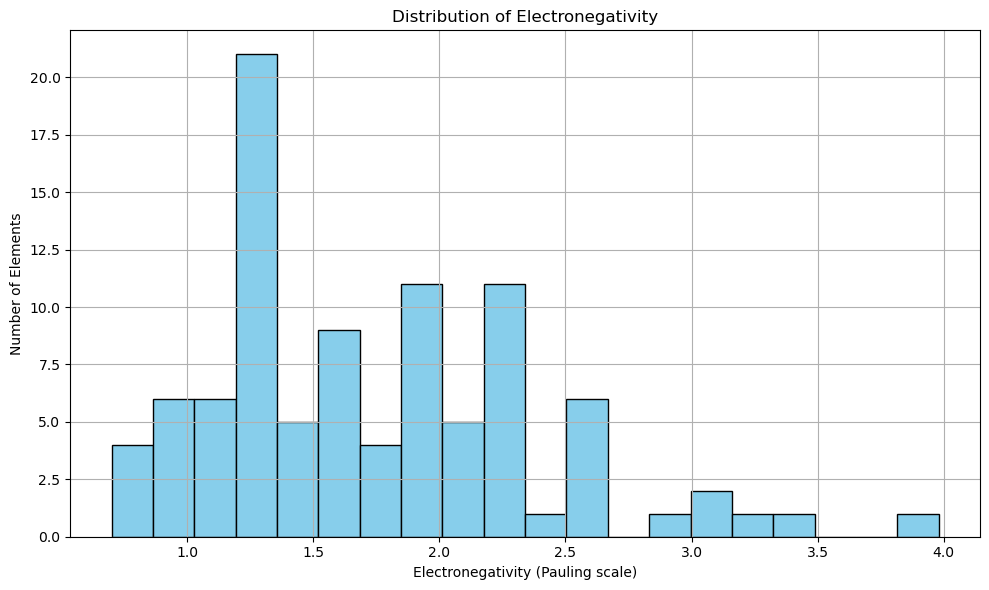
Are most elements electronegative or electropositive?#

import matplotlib.pyplot as plt

# Drop NaN values to avoid errors in plotting
atomic_masses = df_periodictable['Electronegativity'].dropna()

fig, ax = plt.subplots(figsize=(10, 6))
ax.hist(atomic_masses, bins=20, color='skyblue', edgecolor='black')
ax.set_title('Distribution of Electronegativity')
ax.set_xlabel('Electronegativity (Pauling scale)')
ax.set_ylabel('Number of Elements')
plt.grid(True)
plt.tight_layout()
plt.show()
../../_images/4539328a3b403406474f84fc66c1abbd3b99a6cc33dcbdaffc140e9ff7b98aed.png 
import matplotlib.pyplot as plt
import numpy as np

# Clean data: drop rows where any of the required values are missing
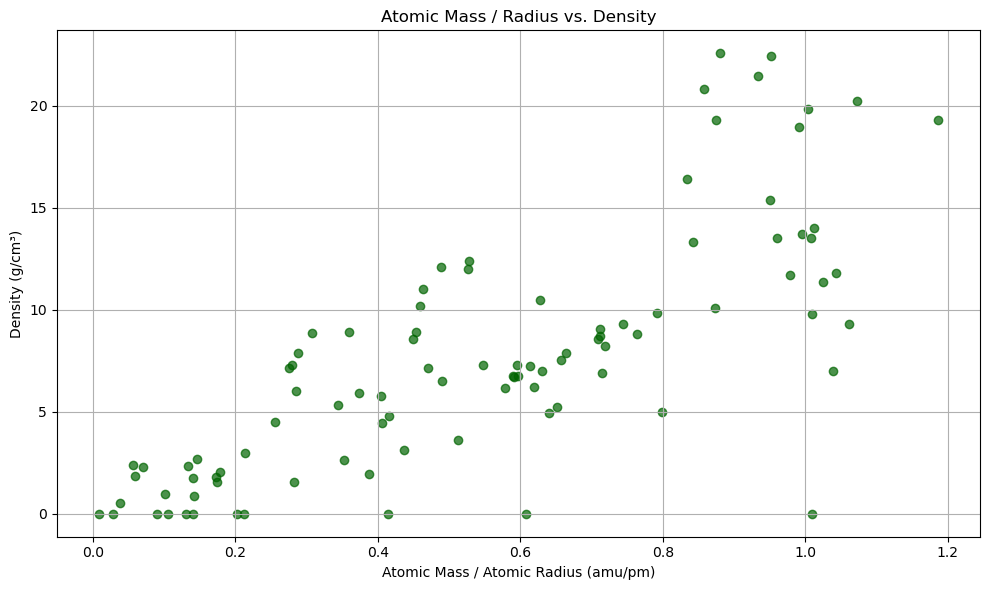
subset_df = df_periodictable[['AtomicMass', 'AtomicRadius', 'Density']].dropna()

# Compute mass/radius
mass_per_radius = subset_df['AtomicMass'] / subset_df['AtomicRadius']
density = subset_df['Density']

# Scatter plot
fig, ax = plt.subplots(figsize=(10, 6))
scatter = ax.scatter(mass_per_radius, density, color='darkgreen', alpha=0.7)

ax.set_title('Atomic Mass / Radius vs. Density')
ax.set_xlabel('Atomic Mass / Atomic Radius (amu/pm)')
ax.set_ylabel('Density (g/cm³)')
ax.grid(True)

plt.tight_layout()
plt.show()
../../_images/01c586178ff4302bf46b220a27b12258d7ae9e5abe5106c9b35692b067a33a29.png 
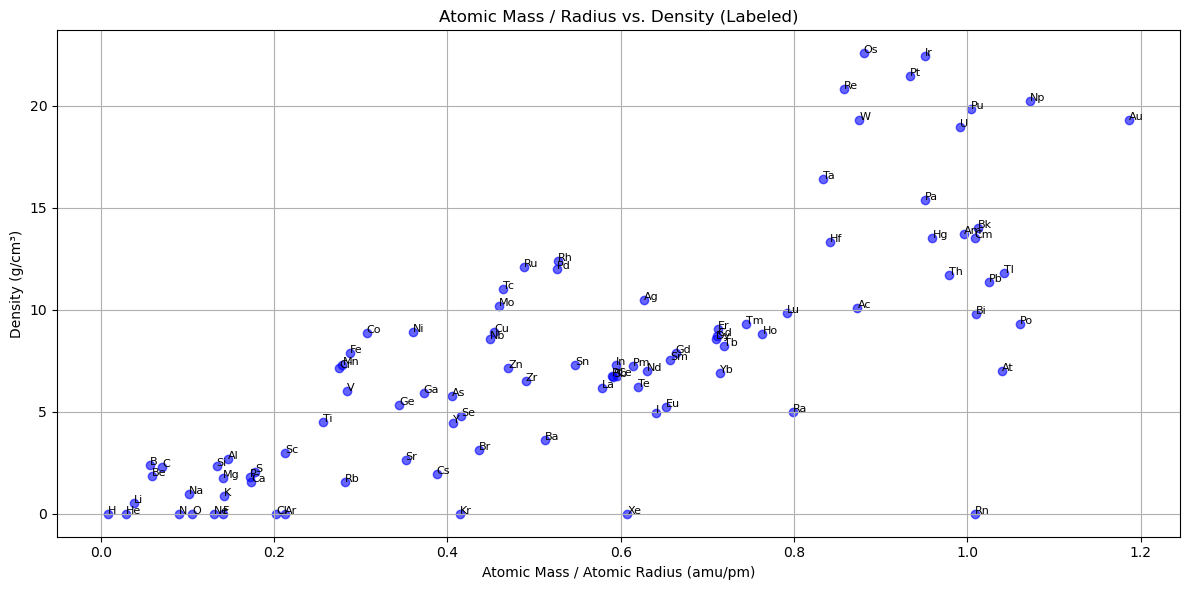
# Get element symbols from index
symbols = subset_df.index

fig, ax = plt.subplots(figsize=(12, 6))
for i in range(len(symbols)):
    ax.scatter(mass_per_radius.iloc[i], density.iloc[i], color='blue', alpha=0.6)
    ax.text(mass_per_radius.iloc[i], density.iloc[i], symbols[i], fontsize=8)

ax.set_title('Atomic Mass / Radius vs. Density (Labeled)')
ax.set_xlabel('Atomic Mass / Atomic Radius (amu/pm)')
ax.set_ylabel('Density (g/cm³)')
ax.grid(True)
plt.tight_layout()
plt.show()
../../_images/e7a90a54eab59a84b0d0adbb24b22b2aacce6a524e32acfff194a1b8064eee40.png 
import matplotlib.pyplot as plt

# Define a color for each GroupBlock
group_colors = {
    'Nonmetal': 'forestgreen',
    'Noble gas': 'mediumslateblue',
    'Halogen': 'goldenrod',
    'Alkali metal': 'crimson',
    'Alkaline earth metal': 'darkorange',
    'Metalloid': 'teal',
    'Post-transition metal': 'darkcyan',
    'Transition metal': 'darkviolet',
    'Lanthanide': 'saddlebrown',
    'Actinide': 'firebrick'
}

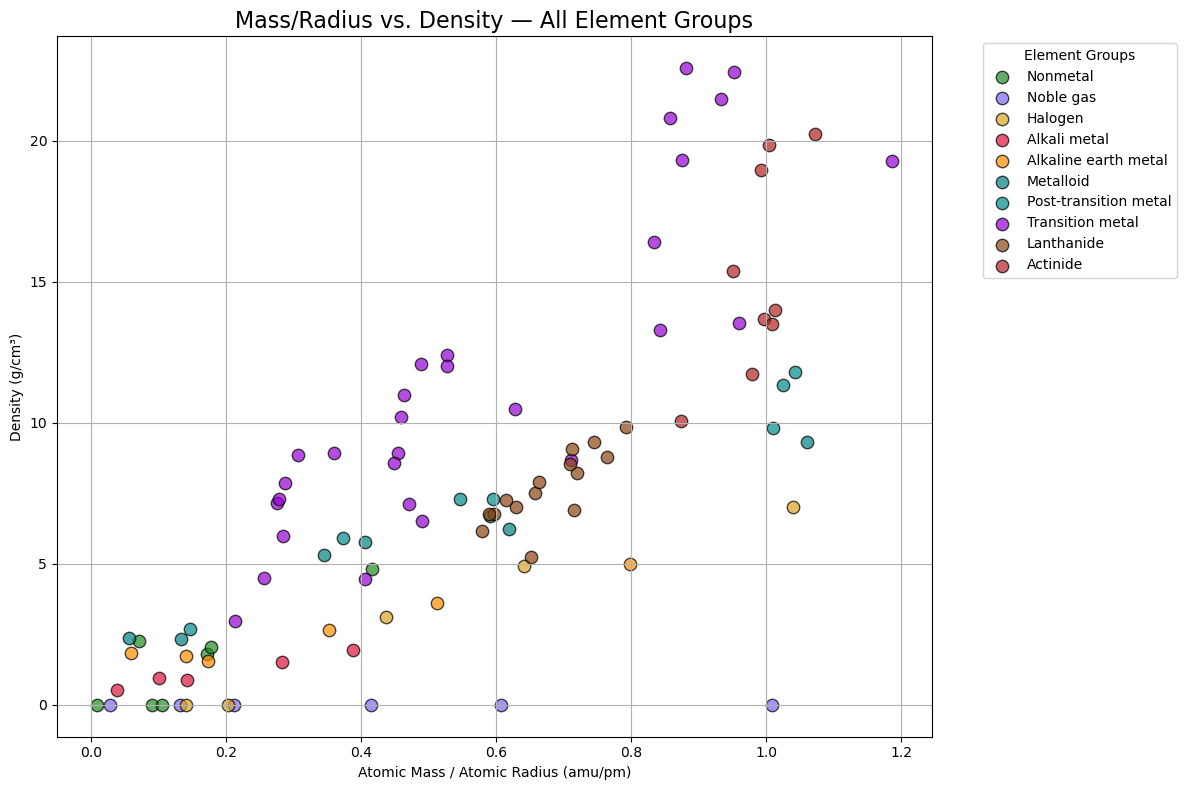
# Create a scatterplot for all elements, color-coded by group
plt.figure(figsize=(12, 8))

for group, color in group_colors.items():
    group_df = df_periodictable[df_periodictable['GroupBlock'] == group]
    
    # Drop rows with NaNs
    clean_df = group_df.dropna(subset=['AtomicMass', 'AtomicRadius', 'Density'])
    
    if clean_df.empty:
        continue  # Skip group if no valid data
    
    mass_per_radius = clean_df['AtomicMass'] / clean_df['AtomicRadius']
    density = clean_df['Density']
    
    # Scatter plot for group
    plt.scatter(mass_per_radius, density, 
                color=color, edgecolor='black', s=80, alpha=0.7, label=group)

# Labels and legend
plt.title('Mass/Radius vs. Density — All Element Groups', fontsize=16)
plt.xlabel('Atomic Mass / Atomic Radius (amu/pm)')
plt.ylabel('Density (g/cm³)')
plt.grid(True)
plt.legend(title='Element Groups', bbox_to_anchor=(1.05, 1), loc='upper left')
plt.tight_layout()
plt.show()
../../_images/265d5bb4e9edc0ec0f5bf86fa9a31b4fb989cc7838a5ea573ee4dcc5b35d4668.png 
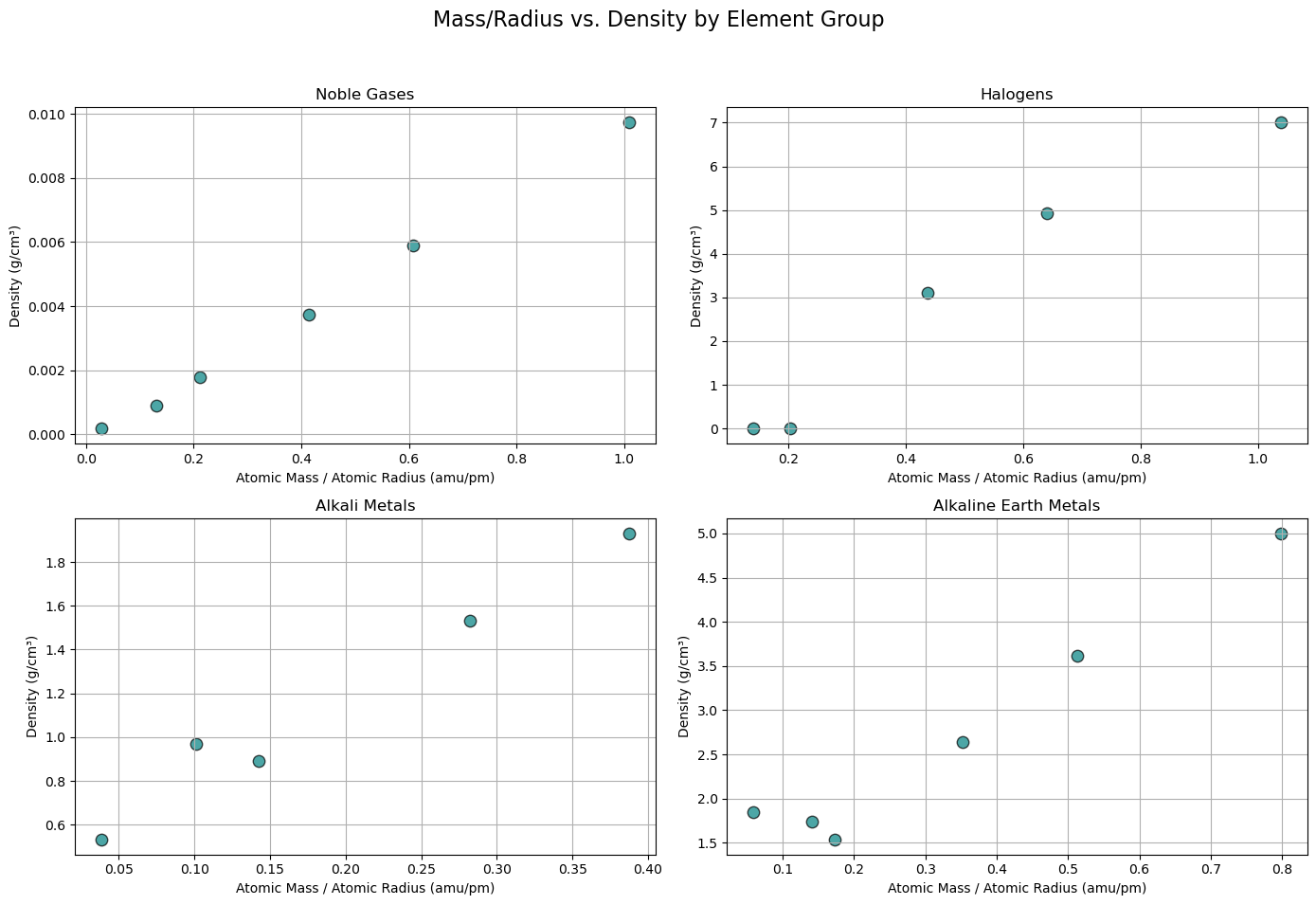
import matplotlib.pyplot as plt

# Updated groups list with correct labels (matching your DataFrame exactly)
groups = [
    ('Noble gas', 'Noble Gases'),
    ('Halogen', 'Halogens'),
    ('Alkali metal', 'Alkali Metals'),
    ('Alkaline earth metal', 'Alkaline Earth Metals')
]

# Set up 2x2 subplot grid
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
axes = axes.flatten()

for i, (group_block, title) in enumerate(groups):
    ax = axes[i]
    
    # Filter DataFrame for this group
    group_df = df_periodictable[df_periodictable['GroupBlock'] == group_block]
    
    # Drop rows with NaNs in key columns
    clean_df = group_df.dropna(subset=['AtomicMass', 'AtomicRadius', 'Density'])
    
    # Debug: Show count before and after dropna
    print(f"{title}: {len(group_df)} total rows, {len(clean_df)} valid rows after dropna")

    if clean_df.empty:
        ax.set_title(f"{title} (No Data)")
        ax.axis('off')
        continue

    # Compute Mass/Radius
    mass_per_radius = clean_df['AtomicMass'] / clean_df['AtomicRadius']
    density = clean_df['Density']

    # Scatter plot
    ax.scatter(mass_per_radius, density, color='teal', edgecolor='black', s=80, alpha=0.7)

    # Labels and grid
    ax.set_title(title)
    ax.set_xlabel('Atomic Mass / Atomic Radius (amu/pm)')
    ax.set_ylabel('Density (g/cm³)')
    ax.grid(True)

# Main title and layout adjustment
plt.suptitle('Mass/Radius vs. Density by Element Group', fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

Noble Gases: 7 total rows, 6 valid rows after dropna
Halogens: 6 total rows, 5 valid rows after dropna
Alkali Metals: 6 total rows, 5 valid rows after dropna
Alkaline Earth Metals: 6 total rows, 6 valid rows after dropna
../../_images/d9a2410aabbd6349031697d535f59c90db84643a29217e98361e4c2b202ee016.png 
print(df_periodictable['GroupBlock'].unique())

['Nonmetal' 'Noble gas' 'Alkali metal' 'Alkaline earth metal' 'Metalloid'
 'Halogen' 'Post-transition metal' 'Transition metal' 'Lanthanide'
 'Actinide']

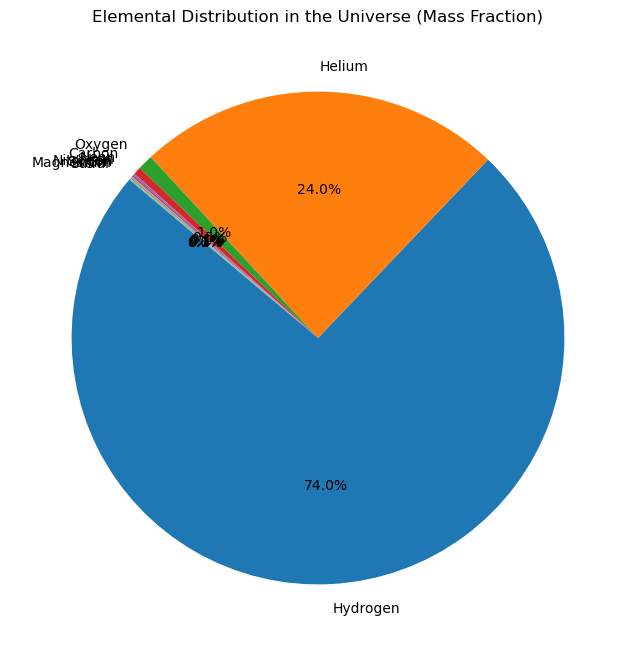
import matplotlib.pyplot as plt

# Data for the pie chart
labels = ['Hydrogen', 'Helium', 'Oxygen', 'Carbon', 'Neon', 'Iron', 'Nitrogen', 'Silicon', 'Magnesium', 'Sulfur']
sizes = [74, 24, 1, 0.5, 0.13, 0.11, 0.09, 0.07, 0.06, 0.05]  # Percentages

# Create the pie chart
plt.figure(figsize=(8, 8))
plt.pie(sizes, labels=labels, autopct='%1.1f%%', startangle=140)
plt.title('Elemental Distribution in the Universe (Mass Fraction)')
plt.show()
../../_images/8f02ea6ca5db76bd089a2266df2301453ee770548132136bad1e08e259170b3e.png

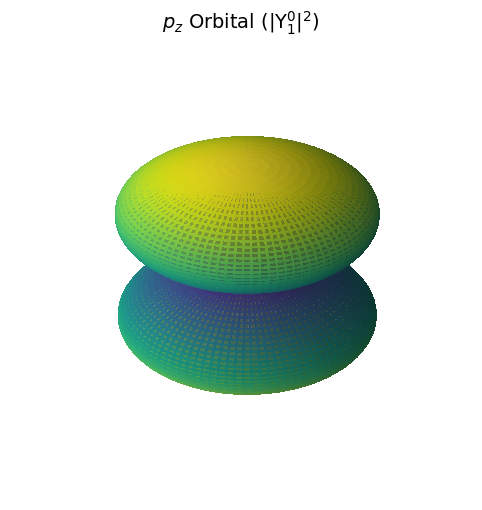
P Orbitals#

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
import warnings

# Suppress the deprecation warning for now
warnings.filterwarnings("ignore", category=DeprecationWarning)

# Spherical coordinates
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2 * np.pi, 100)
theta, phi = np.meshgrid(theta, phi)

# Quantum numbers
l = 1
m = 0

# Spherical harmonic (working version)
Y_lm = sph_harm(m, l, phi, theta)
prob_density = np.abs(Y_lm)**2

# Cartesian conversion
r = prob_density
x = r * np.sin(theta) * np.cos(phi)
y = r * np.sin(theta) * np.sin(phi)
z = r * np.cos(theta)

# Plot
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, facecolors=plt.cm.viridis(prob_density / prob_density.max()),
                rstride=1, cstride=1, antialiased=False, alpha=0.7)

ax.set_title(r'$p_z$ Orbital (|Y$_1^0|^2$)', fontsize=14)
ax.set_axis_off()
plt.show()
../../_images/594d2563cb9b81516b57553093615802352743af74b8f53c2ceba2972f20b7b9.png 
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
import warnings

# Suppress deprecation warning for sph_harm
warnings.filterwarnings("ignore", category=DeprecationWarning)

# Create spherical grid
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2 * np.pi, 100)
theta, phi = np.meshgrid(theta, phi)

# Create figure with 1 row, 3 subplots (3D)
fig = plt.figure(figsize=(18, 6))

# Orbital definitions (label, m, color map)
orbitals = [
    (r'$p_x$', 1, 'Reds'),
    (r'$p_y$', -1, 'Greens'),
    (r'$p_z$', 0, 'Blues')
]

# Loop through orbitals and plot
for i, (label, m, cmap) in enumerate(orbitals, 1):
    # Compute spherical harmonic
    Y_lm = sph_harm(m, 1, phi, theta)
    
    # Real combinations for p_x and p_y
    if m == 1:
        Y_real = np.real(Y_lm - sph_harm(-1, 1, phi, theta)) / np.sqrt(2)
    elif m == -1:
        Y_real = np.imag(sph_harm(-1, 1, phi, theta) + Y_lm) / np.sqrt(2)
    else:
        Y_real = np.real(Y_lm)
    
    prob_density = np.abs(Y_real)
    r = prob_density  # Use |Y| directly for shape
    x = r * np.sin(theta) * np.cos(phi)
    y = r * np.sin(theta) * np.sin(phi)
    z = r * np.cos(theta)

    # Normalize for color mapping
    norm = (r - r.min()) / (r.max() - r.min())

    # Create subplot
    ax = fig.add_subplot(1, 3, i, projection='3d')
    ax.plot_surface(x, y, z, facecolors=plt.cm.get_cmap(cmap)(norm),
                    rstride=1, cstride=1, antialiased=False, alpha=0.9)
    ax.set_title(label, fontsize=14)
    ax.set_box_aspect([1, 1, 1])
    ax.set_axis_off()

# Show entire figure
plt.suptitle("p Orbital Shapes: $p_x$, $p_y$, $p_z$", fontsize=18)
plt.tight_layout()
plt.show()
../../_images/a2c05d3aecb57f26b42eabab193114e19137cc46b91cebd831ac1821fb5a7de2.png 
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
import warnings

# Suppress deprecation warning
warnings.filterwarnings("ignore", category=DeprecationWarning)

# Spherical grid
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2 * np.pi, 100)
theta, phi = np.meshgrid(theta, phi)

# Cartesian coords for sphere surface
x = np.sin(theta) * np.cos(phi)
y = np.sin(theta) * np.sin(phi)
z = np.cos(theta)

# Quantum numbers
l = 1
m_values = [-1, 0, 1]
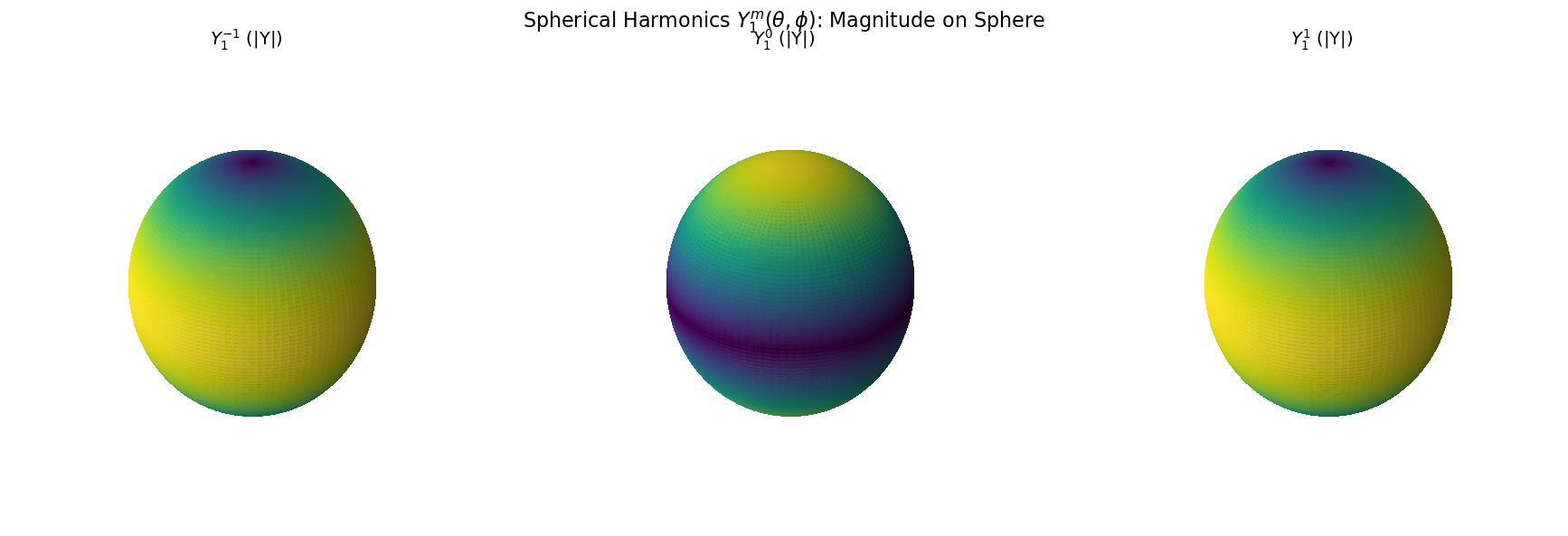
titles = [r'$Y_1^{-1}$', r'$Y_1^{0}$', r'$Y_1^{1}$']

# Create figure
fig = plt.figure(figsize=(18, 6))

for i, m in enumerate(m_values):
    Y_lm = sph_harm(m, l, phi, theta)
    magnitude = np.abs(Y_lm)  # Change to .real or .imag to explore those

    # Normalize for colormap
    mag_norm = (magnitude - magnitude.min()) / (magnitude.max() - magnitude.min())

    # Plot on sphere
    ax = fig.add_subplot(1, 3, i+1, projection='3d')
    ax.plot_surface(x, y, z, facecolors=plt.cm.viridis(mag_norm),
                    rstride=1, cstride=1, antialiased=False, alpha=0.9)
    ax.set_title(f"{titles[i]} (|Y|)", fontsize=14)
    ax.set_box_aspect([1, 1, 1])
    ax.set_axis_off()

plt.suptitle(r"Spherical Harmonics $Y_1^m(\theta, \phi)$: Magnitude on Sphere", fontsize=16)
plt.tight_layout()
plt.show()
../../_images/3bfdf1aa2c33ff36ca3b61ee9cdb52c276bb74b328b4f50136aac4ba9f6e95f1.png 
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import sph_harm
import warnings

# Suppress deprecation warning for sph_harm
warnings.filterwarnings("ignore", category=DeprecationWarning)

# Spherical grid
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2 * np.pi, 100)
theta, phi = np.meshgrid(theta, phi)

# Cartesian coordinates for unit sphere
x = np.sin(theta) * np.cos(phi)
y = np.sin(theta) * np.sin(phi)
z = np.cos(theta)

# Quantum numbers
l = 1
m_values = [-1, 0, 1]
col_titles = [r'$Y_1^{-1}$', r'$Y_1^{0}$', r'$Y_1^{1}$']
row_titles = ['|Y| (Magnitude)', 'Re(Y)', 'Im(Y)']

# Create figure
fig = plt.figure(figsize=(15, 12))
cmap = plt.cm.viridis  # Consistent colormap

# Data fields to loop over
data_types = ['magnitude', 'real', 'imag']

# For colorbars
colorbars = []

for i, data_label in enumerate(data_types):
    all_fields = []  # Collect all values in row for colorbar range

    # First pass: collect data for normalization range
    for m in m_values:
        Y_lm = sph_harm(m, l, phi, theta)
        if data_label == 'magnitude':
            field = np.abs(Y_lm)
        elif data_label == 'real':
            field = Y_lm.real
        elif data_label == 'imag':
            field = Y_lm.imag
        all_fields.append(field)

    # Determine global min/max for the row
    combined = np.concatenate([f.flatten() for f in all_fields])
    global_min, global_max = combined.min(), combined.max()

    # Avoid divide by zero
    if np.isclose(global_max, global_min):
        global_max = global_min + 1e-8

    # Second pass: plot with consistent normalization
    for j, field in enumerate(all_fields):
        norm = (field - global_min) / (global_max - global_min)

        ax = fig.add_subplot(3, 3, i * 3 + j + 1, projection='3d')
        surf = ax.plot_surface(x, y, z, facecolors=cmap(norm),
                               rstride=1, cstride=1, antialiased=False, alpha=0.9)
        ax.set_box_aspect([1, 1, 1])
        ax.set_axis_off()

        if i == 0:
            ax.set_title(col_titles[j], fontsize=12)
        if j == 0:
            ax.text2D(-0.1, 0.5, row_titles[i], fontsize=12, rotation=90,
                      transform=ax.transAxes, va='center', ha='center')

    # Add shared colorbar for the row
    cbar_ax = fig.add_axes([0.92, 0.7 - i * 0.3, 0.015, 0.2])  # Position on the right
    sm = plt.cm.ScalarMappable(cmap=cmap)
    sm.set_array(combined)
    sm.set_clim(global_min, global_max)
    cbar = fig.colorbar(sm, cax=cbar_ax)
    cbar.set_label(row_titles[i], fontsize=10)

plt.suptitle("Spherical Harmonics $Y_1^m(\\theta, \\phi)$: Magnitude, Real, Imaginary Parts with Colorbars", fontsize=16)
plt.subplots_adjust(left=0.05, right=0.9, top=0.95, bottom=0.05, wspace=0.3, hspace=0.3)

plt.show()
../../_images/843e26e1a31d2e025de3eb48de3799f85f86cbbbf85307fbbc65d1360ebfa615.png

Acknowldegments#

Material in this activty has been adapted from chapter 3 of Charles Weiss’s book “Scientific Computing for Chemists with Python”, CC BY-NC-SA 4.0.

Additional content was developed with assistance from Perplexity AI and Chat GPT. Multiple queries were made during the Fall 2024 and the Spring 2025.

Contents